Феликс Филатов - Клеймо создателя

При метеоритных ударах таких масштабов возникали трещины, из которых выделялась горячая вода, насыщенная органическими молекулами, и такие трещины могли стать очагами предбиологических процессов, которые привели к быстрому появлению жизни по окончании бомбардировки.

Жизнь могла возникнуть именно в горячей воде таких гидротермальных очагов. По мнению Кринга и Коэна, условия в трещинах метеоритов были настолько благоприятными для этого, что первые живые клетки могли появиться там уже через несколько сот тысяч лет после конца бомбардировки, то есть примерно 3,85 миллиардов лет тому назад. Эта дата, действительно, близка к возрасту обнаруженных в последние годы первых признаков жизни на Земле.

…………………

Немного о номере этой главы. Читатель, который уже ожидал, что им станет число 31 , поскольку очевидная привязанность Автора к триплету 111 , как будто, требует перехода от представления этого гомотриплета в четверичной системе ( 21 ) к представлению его в пятеричной, будет приятно разочарован доверием Автора к своей сообразительности. Автор принимает, что Читатель давно усвоил и само понятие о системах счисления, и «равноправие» таких систем с различными основаниями. Другое дело – человеческая культура, где некоторые из этих систем исторически акцентированы (например, десятичная, как удобная для счета пальцами обеих рук, или пятеричная, которую – из тех же соображений – еще в XIX веке использовали китайцы, освободив другую руку для других дел). Гомотриплет (информационная сигнатура с тремя одинаковыми знаками) 111 выделен в таблице ниже, в которой – как и в предыдущем случае ( Глава 21 ), но уже для пятеричной системы – он соответствует децимальному числу 31 . Первые тридцать пять десятичных чисел (темные колонки) в пятеричной системе счисления записываются так (светлые колонки):

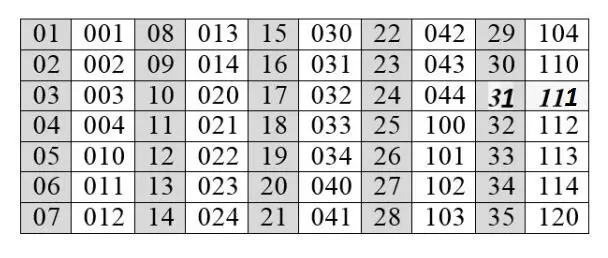
В соответствии с определением, пятеричная система счисления использует пять символов-цифр: 1, 2, 3, 4 и 0.

Вместо того, чтобы утомлять читателя однотипным комментарием, посвящая его номеру очередной главы, который соответствует одному и тому же числу в очередной системе счисления, Автору кажется гораздо выигрышней сразу представить это число общей таблицей в серии систем с основаниями от 1 до 20 (крупный шрифт – десятичные числа N, соответствующие числу 111 в системах счисления, основания которых, P , обозначены мелким шрифтом):

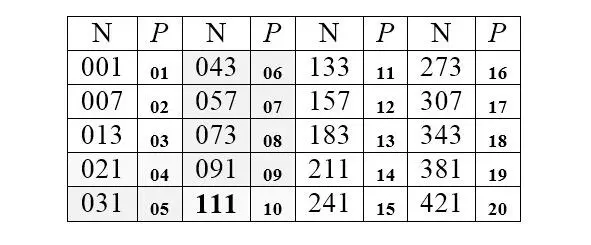
Таблица, естественно, открывается числом 1. Система счисления с основанием 1 системой в принятом смысле, вообще говоря, не является. Число 1111 в такой «системе» графически означает всего лишь десятичную тройку ( 3= 1+ 1+ 1), соответствующую тройке римской – III(числу без разрядов). Таким же образом десятичному 111 соответствуют сто одиннадцать символов 1 , представленных также без всяких разрядов, поскольку символа ноля в « сингулярной » (унарной) системе нет. Вот как оно выглядит (для удобства восприятия это число изображено тремя равными строками по 37 единиц):

1111111111111111111111111111111111111

1111111111111111111111111111111111111

1111111111111111111111111111111111111

Обратив, таким образом, внимание на число 1 и вспомнив о прошлом человечества, когда сингулярная система счисления была и единственной, и единственно возможной, Автор и главу эту хотел было обозначить приведенным трехстрочным числом. Но ни три римские цифры, ни три строки цифр арабских не показались ему уместными или «соответствующими» в контексте рассказа, и он ограничился «одноразрядным» числом, графемой (или нумералом ) 1 . Да и навязчивым быть не хотелось со своими предпочтениями – до поры, до времени.

Мы уже упоминали об особенности четверичного числа 111 4 (21) – способности делиться без остатка на три. Такой же способностью обладает семеричное число 111 7 ( 57 ) и десятичное 111 (системы с Р > 10 мы здесь не рассматриваем). Наибольшие общие делители d каждого из этих чисел равны: 7 = 13 4, 19 = 25 7 и 37 = 37 10 . Делимость трехзначного числа в этих системах на d следует прямой (слева направо) пермутации: если на 37 (в системе P =10) делится, например, число 925, то тем же свойством обладают также числа 259 и 592 (но не 529 и не 295). Из этого следует делимость на 37 всех гомотриплетов – 111 , 222 , 333 и т. д. Те же рассуждения справедливы и в отношении чисел четверичной и семеричной систем. Владимир Щербак упоминает Луку Пачиоли, известного математика Возрождения, «изобретателя» бухгалтерского учета, друга и учителя математики самого Леонардо, которого « изумила цифровая симметрия десятичных чисел, кратных 37 … Если одна из целей такой симметрии – привлечь внимание исследователя, то реакция Пачиоли говорит, что эта цель достижима ». Привлечет ли такое же ИХ внимание позолоченная пластинка «Вояджера»?

Гипотезы о происхождении жизни на Земле исходят в основном из двух предположений. Это либо гипотеза панспермии (что многих не устраивает, поскольку, как они полагают, она лишь отодвигает событие в прошлое и не решает задачу), либо кажущееся гораздо более вероятным предположение о том, что на Земле земная жизнь и возникла. Варианта первой гипотезы мы коснемся позже (ему эта книга и посвящена), что до вероятного предположения , то его сторонники справедливо полагают, что его подтверждением может быть только эксперимент. Именно так считал и Виталий Гинзбург. «В настоящее время мы полагаем, – говорил он, – что знаем, из чего устроено все живое – из электронов, атомов и молекул 46. Знаем строение атомов и молекул, а также управляющие ими и излучением законы. Поэтому естественна гипотеза о редукции – возможности все живое объяснить на основе физики, уже известной физики. Образование в условиях, царивших на Земле несколько миллиардов лет назад, сложных органических молекул уже прослежено, понято и смоделировано . Казалось бы, переход от таких молекул и их комплексов к простейшим организмам, к их воспроизводству можно себе представить. Но здесь имеется какой-то скачок, фазовый переход. Проблема не решена, и я склонен думать, будет безоговорочно решена только после создания жизни в пробирке» . Две выделенные здесь фразы требуют комментария. Сложные органические молекулы , о которых говорится в первой из них, свидетельствуют, конечно, о прогрессе в обсуждаемой области, однако, это еще слишком простая сложность (прошу прощения за невольный каламбур), и ее для обозначенных целей совершенно недостаточно. Уровень сложности , необходимый для моделирования возникновения жизни, определяется не только сложностью самих молекул (то есть числом и разнообразием атомов, их составляющих). Эти молекулы должны объединяться в реакционные циклы и гиперциклы и катализировать их звенья. При этом они должны быть способны формировать цепочки (линейные полимеры), которые – в свою очередь – должны быть способны сохранять информацию и дублировать ее – с ошибками, частота которых не должна превышать значения, позволяющего лишь немного модифицировать исходный контент для отбора оптимального варианта. Ничего похожего в пробирке пока не создано. Совсем недавно удалось химическим путем «собрать» рибонуклеотид, один из четырех основных «кирпичиков», из которых «сделана» РНК. Очень долгое время и эту задачу решить не удавалось. Гинзбург определенно оценивал ситуацию более оптимистично, чем она есть. Второй комментарий касается создания «жизни в пробирке» . Мы уже говорили, что в привычном смысле эксперимент по созданию жизни в пробирке , скорее всего, бесперспективен. Для этого требуются другие пространственные масштабы – как минимум, масштаб планеты или, скорее, планетной системы. Временн ы е масштабы также придется увеличить: очень возможно, что для такого эксперимента потребуются те же 3—4 миллиарда лет. О том, чт о надо будет сделать экспериментатору, чтобы оценить результат своей работы, мы вспомним позже, а пока отметим, что чудовищные расстояния, отделяющие нас от планетных систем, где возможна иная жизнь, вполне могут служить эквивалентом стеклянной стенки пробирки , отделяющей мир экспериментатора от нашего собственного и надежно предупреждающей возможную взаимную контаминацию живым материалом.