Стивен Вайнберг - Объясняя мир. Истоки современной науки

В Граце Кеплер начал переписываться с Тихо Браге, который прочитал «Тайну мироздания». Тихо пригласил Кеплера приехать к нему в Ураниборг, но Кеплер решил, что это было бы слишком далекое путешествие. Позже, в феврале 1600 г., Кеплер принял предложение Браге и приехал к нему в Прагу, которая с 1583 г. стала столицей Священной Римской империи. Там Кеплер начал изучать собранную Тихо информацию, особенно касающуюся движения Марса, и нашел расхождение в 0,13° с расчетами, построенными на теории Птолемея {190}.

Кеплер и Браге не слишком хорошо ладили, и Кеплер вернулся в Грац. Как раз в это время протестанты были изгнаны из Граца, и в августе 1600 г. Кеплер и его семья были вынуждены уехать. Вернувшись в Прагу, Кеплер начал сотрудничать с Тихо в работе над «Рудольфовыми таблицами», новыми астрономическими таблицами, которые должны были заменить «Прусские таблицы» Рейнгольда. После смерти Браге в 1601 г. карьерные проблемы Кеплера были на какое-то время решены, поскольку он стал преемником Тихо на посту придворного математика императора Рудольфа II.

Император очень интересовался астрологией, поэтому в обязанности Кеплера как придворного математика входило составление гороскопов. Эта была работа, в которой он преуспел, еще будучи студентом в Тюбингене, несмотря на свое скептическое отношение к астрологическим предсказаниям. К счастью, у Кеплера оставалось время и для того, чтобы заниматься настоящей наукой. В 1604 г. он наблюдал сверхновую в созвездии Змееносца. Подобного явления в нашей Галактике или около нее после не случалось до 1987 г. В том же году он опубликовал труд «Оптическая часть астрономии» (Astronomiae Pars Optica), посвященный теории оптики и ее приложению к астрономии, включая влияние эффекта рефракции в атмосфере во время наблюдения за движением планет.

Кеплер продолжил работу над теорией движения планет, безуспешно раз за разом пытаясь примирить схему Коперника с точной информацией Браге, добавляя эксцентры, эпициклы и экванты. Он закончил эту работу к 1605 г., но ее публикация была задержана из-за трений с наследниками Тихо. В конце концов в 1609 г. Кеплер опубликовал свои результаты в книге «Новая астрономия, причинно обоснованная, или Небесная физика, основанная на комментариях к движениям звезды Марс».

Часть III «Новой астрономии» вносит существенное уточнение в теорию Коперника – там вводится эквант и эксцентр для Земли. Таким образом, появляется точка, находящаяся с противоположной стороны от центра Земли относительно ее орбиты. Относительно этой точки Земля обращается с постоянной угловой скоростью. Благодаря этому Кеплер избавился от большинства неточностей, которыми изобиловали теории планетного движения со времен Птолемея. Но информация, собранная Браге, была настолько точна, что Кеплер мог видеть: расхождения между теорией и наблюдением по-прежнему остаются.

В какой-то момент Кеплер начал подозревать, что эта задача не имеет решения и что ему следует отказаться от общего для Платона, Аристотеля, Птолемея, Коперника и Браге предположения о том, что планеты движутся по круговым орбитам. Вместо этого он пришел к выводу, что орбиты имеют овальную форму. В конце концов в главе 58 (всего их было 70) «Новой астрономии» Кеплер вывел точное решение. В положении, которое позже стало известно как Первый закон Кеплера, он заключает, что планеты (в том числе и Земля) обращаются по эллиптическим орбитам, при этом Солнце находится в одном из фокусов, а не в центре. Так же как круг может быть полностью определен одной величиной (если не говорить о его положении) – своим радиусом, так и эллипс может быть определен (если не говорить о его положении и ориентации) двумя величинами – длиной малой и большой осей или длиной большой оси и числом, которое называется эксцентриситет , указывающим, насколько различаются большая и малая оси (см. техническое замечание 18). Два фокуса эллипса – это точки на большой оси, равноудаленные от центра и отстоящие друг от друга на расстояние, равное эксцентриситету эллипса, умноженному на длину большой оси. При нулевом эксцентриситете обе оси имеют равную длину, два фокуса сходятся в одной точке и эллипс превращается в окружность.

В действительности орбиты всех планет, известных Кеплеру, имели маленький эксцентриситет, как показано в следующей таблице, где приведены современные (к началу XX в.) значения:

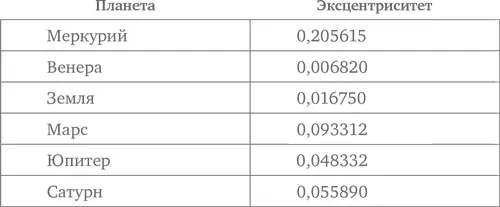
Именно поэтому простейшие версии теорий Коперника и Птолемея (без эпициклов в теории Коперника и только с одним эпициклом для каждой из пяти планет в теории Птолемея) работали достаточно хорошо {191}.

Замена круговых орбит эллипсами повлекла серьезные последствия еще по одной причине. Окружности порождаются движением точек на поверхности сферы, но не существует ни одного твердого тела, в результате вращения которого может получиться эллипс. Это вместе с выводами Браге по поводу кометы 1577 г. привело к краху древней идеи о том, что планеты крепятся к вращающимся сферам, идеи, которую сам Кеплер еще допускал в своей «Тайне мироздания». Вместо этого теперь Кеплер и его последователи считали, что планеты двигаются по орбитам, свободно пролегающим в пустоте космоса.

Вычисления, описанные в «Новой астрономии», также использовались для доказательства положения, которое стало позже известно как Второй закон Кеплера, хотя он не был четко сформулирован до выхода в 1621 г. его «Краткого изложения коперниканской астрономии». Второй закон Кеплера объясняет, как скорость планеты меняется по мере ее движения по орбите. Он гласит, что при движении каждой планеты за равные промежутки времени радиус-вектор, то есть линия, соединяющая Солнце и планету, покрывает равные площади. Когда планета находится близко к Солнцу, она должна двигаться быстрее, чтобы покрыть ту же площадь, за равный промежуток времени, оказавшись далеко от Солнца. Таким образом, следствием из Второго закона Кеплера является то, что планеты ускоряются, приближаясь к Солнцу. Если не считать мелких поправок, пропорциональных квадрату эксцентриситета, то Второй закон Кеплера означает, что радиус-вектор от планеты до другого фокуса ее орбиты (того, в котором нет Солнца) вращается с постоянной угловой скоростью – то есть она поворачивается на один и тот же угол каждую секунду (см. техническое замечание 21). Таким образом, с хорошей точностью закон Кеплера дает те же планетные скорости, что и древняя идея экванта – точки, расположенной на противоположной стороне от центра окружности относительно Солнца (или, по Птолемею, относительно Земли) и находящейся на том же расстоянии от центра, вокруг которой линия, ведущая к планете, вращается с постоянной угловой скоростью. Следовательно, эквант оказывается ничем иным как пустым фокусом эллипса. Только великолепная коллекция наблюдений Браге за положением Марса позволила Кеплеру прийти к выводу, что эксцентра и экванта недостаточно и что круговые орбиты должны быть заменены эллиптическими {192}.