Леонард Сасскинд - Космический ландшафт. Теория струн и иллюзия разумного замысла Вселенной

Возвращаясь к своему словарю, я нахожу в нём следующее определение слова «изотропный»: одинаковый во всех направлениях; инвариантный относительно направления . «Изотропный» не то же самое, что «однородный». Приведу пример. Однажды, во время погружения с аквалангом на одном из коралловых рифов в Красном море я увидел огромную стаю узких длинных рыб, однородно заполнявших большой объём. Но по какой-то необъяснимой причине, пока я находился слишком близко, все рыбы были повёрнуты в одну и ту же сторону. Косяк был однородным на определённом масштабе, но он определённо не был изотропным. Любой фрагмент косяка выглядел точно так же, как и любой другой фрагмент этого же косяка, но этого нельзя было сказать про направление, в котором смотрели рыбы.

Космологи и астрономы предполагают, что Вселенная является однородной и изотропной: независимо от того, в каком месте Вселенной вы находитесь и в каком направлении смотрите, вы видите одно и то же. Я имею в виду не близлежащие детали, а крупномасштабные особенности Вселенной. Космологи называют это предположение «космологическим принципом». Конечно, от того, что мы назвали его принципом, оно автоматически не стало истинным. Первоначально это была просто гипотеза, но всё более тщательные и разнообразные наблюдения убедили астрономов и космологов, что Вселенная действительно однородна и изотропна на масштабах от нескольких сотен миллионов до, по крайней мере, нескольких десятков миллиардов световых лет. О свойствах Вселенной на ещё больших расстояниях мы ничего не можем сказать, потому что четырнадцать миллиардов световых лет – это предел наших наблюдательных возможностей. Независимо от того, насколько большой телескоп мы возьмём, мы не сможем увидеть объект на расстоянии больше четырнадцати миллиардов световых лет. Причина состоит в том, что возраст самой Вселенной составляет около четырнадцати миллиардов лет. За это время свет может пройти расстояние не более четырнадцати миллиардов световых лет. Свет от более далёких объектов просто ещё не успел до нас добраться. На самом деле ставка на то, что Вселенная является однородной и изотропной на расстояниях, превышающих размеры наблюдаемой части Вселенной, может и сыграть, но, подобно сельской местности, Вселенная может оказаться похожей на больших расстояниях на лоскутное одеяло: лоскутное одеяло, сшитое из карманных вселенных.

Пока же примем как рабочее предположение господствующую точку зрения, что космологический принцип справедлив вплоть до самых больших расстояний. Оно подводит нас к интересному вопросу: какая геометрия пространства совместима с космологическим принципом? Под геометрией пространства я имею в виду форму пространства. Начнём с двумерных примеров. 2-сфера является частным случаем геометрии. Помимо сферы пространство может иметь форму эллипсоида, груши и банана. [52]

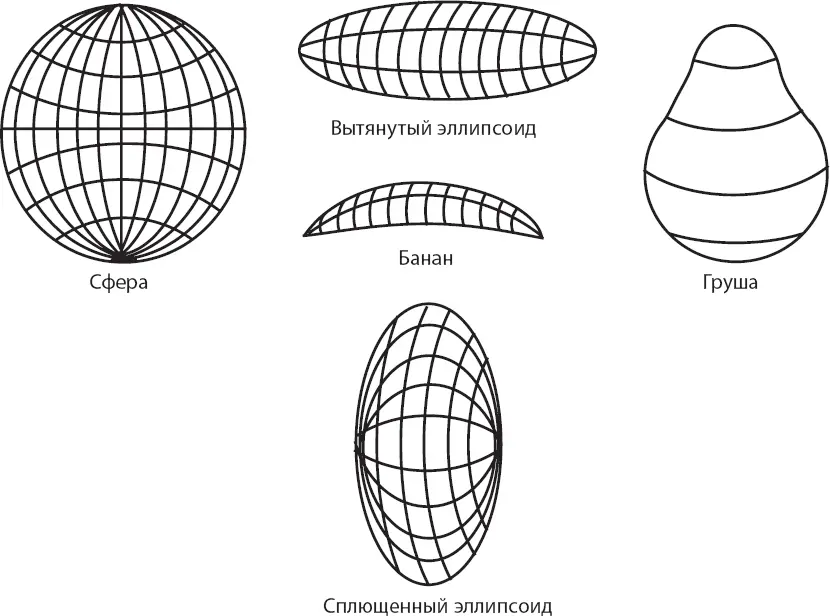
Из всех перечисленных объектов однородна и изотропна только сфера. Она, подобно окружности, обладает совершенной симметрией: каждая точка сферы ничем не отличается от другой точки сферы. Эллипсоид, хотя и не так совершенен, как сфера, всё ещё остаётся достаточно симметричной фигурой. Например, зеркальное отражение эллипсоида ничем не отличается от оригинала. Но уже далеко не каждый участок поверхности эллипсоида неотличим от других. Груша или банан ещё менее симметричны.

Одним из способов описания поверхности является указание её кривизны. Кривизна сферы абсолютно однородна. Говоря математическим языком, сфера является пространством с однородной положительной кривизной. Эллипсоид тоже обладает всюду положительной кривизной, однако его кривизна меняется от одного места поверхности к другому. Например, вытянутый эллипсоид, форма которого напоминает подводную лодку, имеет бо́льшую кривизну на концах и меньшую посередине. Из всех примеров одна только сфера имеет всюду постоянную кривизну.

Сферы, эллипсоиды и поверхности фруктов замкнуты и ограниченны – это означает, что они имеют конечную площадь, но не имеют краёв. Но следует признать, что никто не знает, конечна ли Вселенная, ведь до сих пор не нашлось космического Магеллана, который совершил бы круговселенское путешествие. Поэтому вполне возможно, что Вселенная продолжается неограниченно далеко, и в этом случае она бесконечна и безгранична.

В том случае, если мы считаем Вселенную бесконечной, возможны две однородные и изотропные геометрии Вселенной. Первая, очевидно, представляет собой бесконечное плоское пространство. Представьте себе бесконечный во всех направлениях плоский лист бумаги. На бесконечной плоскости нет никаких выделенных точек, о которых можно было бы сказать, что они находятся ближе к центру или ближе к краю. Но в отличие от сферы, плоскость не имеет кривизны, или, говоря математическим языком, кривизна плоскости равна нулю. Итак, мы знаем две однородные геометрии: сфера с положительной кривизной и плоскость с нулевой кривизной. Остаётся ещё третий вариант: гиперболоид с отрицательной кривизной. Чтобы вообразить поверхность с отрицательной кривизной, представьте себе кусок водопроводной трубы, согнутый под прямым углом. С внешней стороны «локтя» поверхность металла имеет положительную кривизну, как сфера. Кривизна же поверхности на внутренней стороне изгиба отрицательна.

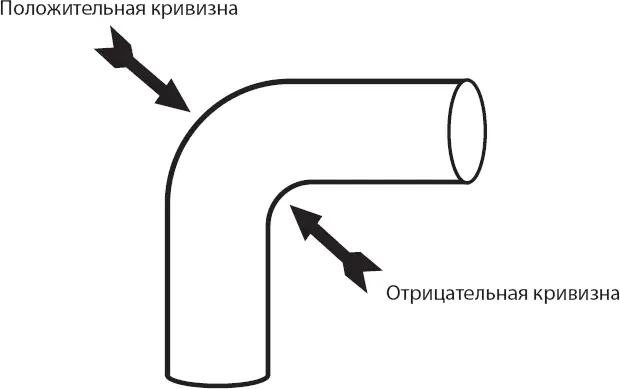
Конечно же, колено водопроводной трубы неоднородно. Внутренняя сторона колена геометрически не похожа на внешнюю, потому что их кривизны имеют разные знаки. Лучшим примером поверхности с отрицательной кривизной служит поверхность седла: представьте себе седло, поверхность которого неограниченно поднимается вверх спереди и сзади от седока и неограниченно спускается вниз справа и слева, – и вы получите представление о бесконечной поверхности, имеющей всюду отрицательную кривизну.

Все три поверхности – сфера, плоскость и гиперболоид – однородны. Более того, все три поверхности имеют аналоги в трёхмерном пространстве: 3-сфера, обычное трёхмерное евклидово пространство и более трудное для представления трёхмерное гиперболическое пространство.

Теперь, когда мы представляем себе три стандартных типа космологии, предположим, что каждая из поверхностей представляет собой резиновую плёнку (или резиновый шарик для случая сферы) с нарисованными на ней галактиками. Начав равномерно растягивать плёнку, мы убедимся, что расстояния между двумя любыми галактиками будут изменяться, следуя закону Хаббла. Теперь у вас есть примерное представление о трёх возможных однородных и изотропных космологических моделях. Космологи обозначают эти модели числом k , принимающим значения 1, 0 и –1 соответственно для положительной кривизны (сферы), нулевой кривизны (плоскости) и отрицательной кривизны (гиперболоида).