Аурика Луковкина - Высшая математика. Шпаргалка

Функциональный ряд называется равномерно сходящимся на множестве М к функции S ( x ), если для всякого положительного ε найдется такое число N , что для всех n > N и для всех х , принадлежащих множеству М , справедливо неравенство:

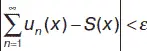
Теорема.Если члены ряда u n ( x ) – непрерывные функции и ряд на множестве М сходится равномерно, то и S ( x ) = u n ( x ) является непрерывной функцией.

Степенным рядомназывается функциональный ряд вида а 0+ а 1( х – х 0) + а 2( х – х 0) 2+…+ а n ( x – x 0) n +… = 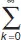a k ( x – x 0) k . Числа a i ( i = 0, 1, 2…) называются коэффициентами ряда. Число R называется радиусом сходимости.

Свойства степенных рядов.

Теорема 1.Если степенной ряд 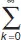a k ( x – x 0) k имеет радиус сходимости R , то в любом круге комплексной плоскости (или на любом отрезке вещественной оси) вида | x – x 0| < r, r < R он равномерно сходится.

Теорема 2.Если для степенного ряда 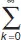a k ( x – x 0) k существует предел 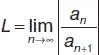, то он равен радиусу сходимости данного ряда, т. е. L = R .

Следствие.

1. На множестве { x | | x – x 0| < r }, r < R сумма степенного ряда является непрерывной функцией.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.