Аурика Луковкина - Высшая математика. Шпаргалка

Координата точки– это величина, определяющая положение данной точки на плоскости, на прямой или кривой линии или в пространстве. Значение координаты зависит от выбора начальной точки, от выбора положительного направления и от выбора единицы масштаба.

Прямоугольная система координатсостоит из двух взаимно перпендикулярных прямых – осей, точка их пересечения – начало координат О , ось ОХ – ось абсцисс, ось ОY – ось ординат. На осях выбираются масштаб и положительное направление.

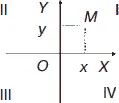
Рис. 1

Системы координат

Положение точки М определяется двумя координатами: абсциссой х и ординатой у . Записывается так: М ( х, у ). Оси координат образуют четыре координатных угла I, II, III, IV. Если точка находится в I координатном угле (квадранте), то и абсцисса, и ордината ее положительные, если – во II квадранте, то абсцисса отрицательна, а ордината положительна, если в – III квадранте, и абсцисса, и ордината отрицательны, если – в IV квадранте, положительна абсцисса, а ордината отрицательна. У точки, лежащей на оси ординат, абсцисса равна нулю, и наоборот, если точка лежит на оси абсцисс, то ее ордината равна нулю.

Косоугольной системой координатаналогична прямоугольной, только оси координат пересекаются под углом не равным прямому. Прямоугольная и косоугольная системы относятся к декартовой системе координат.

Полярная система координатсостоит из полюса О и полярной оси ОХ , проведенной из полюса. Положение точки определяется полярным радиусом ρ (отрезок ОМ ) и полярным углом φ . Для полярного угла берется его главное значение(от – π до π ). Числа ρ, φ называются полярными координатамиточки М .

Связь между координатами точки в прямоугольной и полярной системах координат: x = r cos φ, y = r sin φ или:

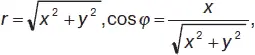
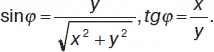
Пусть имеются две точки М 1( х 1, у 1) и М 2( х 2, у 2). Расстояние между точками:

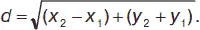
Общее уравнение прямой линии(система координат прямоугольная) : Ах + Ву + С = 0 ( А и В одновременно не равны нулю).

Если В не равно нулю, то уравнение прямой: у = ах + b (здесь а = – А / В, b = – С / В ). Здесь а есть тангенс угла наклона прямой к положительному направлению оси абсцисс, b равно длине отрезка от начала координат до точки пересечения рассматриваемой прямой с осью ординат. Уравнение прямой, параллельной оси абсцисс: у = b , уравнение оси абсцисс: у = 0; уравнение прямой, параллельной оси ординат: х = с , уравнение оси ординат: х = 0.

1. Пусть даны три точки А 1( х 1, у 1), А 2( х 2, у 2), А 3( х 3, у 3), тогда условие нахождения их на одной прямой:

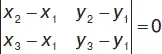
либо ( х 2– х 1) ( у 3– у 1) – ( х 3– x 1) ( у 2– у 1) = 0.

2. Пусть даны две точки А 1( х 1, у 1), А 2( х 2, у 2), тогда у равнение прямой, проходящей через эти две точки:

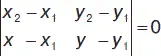
( х 2– х 1)( у – у 1) – ( х – х 1)( у 2– у 1) = 0 или ( х – х 1) / ( х 2– х 1) = ( у – у 1) / ( у 2– у 1).

3. Пусть имеются точка М ( х 1, у 1) и некоторая прямая L , представленная уравнением у = ах + с . Уравнение прямой, проходящей параллельно данной прямой L через данную точку М:

у – у 1= а ( х – х 1).

Если прямая L задана уравнением Ах + Ву + С = 0, то параллельная ей прямая, проходящая через точку М , описывается уравнением А ( х – х 1) + В ( у – у 1) = 0.

Уравнение прямой, проходящей перпендикулярно данной прямой L через данную точку М :

у – у 1= –( х – х 1) / а

или

а ( у – у 1) = х 1– х .

Если прямая L задана уравнением Ах + Ву + С = 0, то параллельная ей прямая, проходящая через точку М ( х 1, у 1), описывается уравнением А ( у – у 1) – В ( х – х 1) = 0.

4. Пусть даны две точки А 1( х 1, у 1), А 2( х 2, у 2) и прямая, заданная уравнением Ах + Ву + С = 0. Взаимное расположение точек относительно этой прямой:

1) точки А 1, А 2лежат по одну сторону от данной прямой, если выражения ( Ах 1+ Ву 1+ С ) и ( Ах 2+ Ву 2+ С ) имеют одинаковые знаки;

2) точки А 1, А 2лежат по разные стороны от данной прямой, если выражения ( Ах 1+ Ву 1+ С ) и ( Ах 2+ Ву 2+ С ) имеют разные знаки;

3) одна или обе точки А 1, А 2лежат на данной прямой, если одно или оба выражения соответственно ( Ах 1+ + Ву 1+ С ) и ( Ах 2+ Ву 2+ С ) принимают нулевое значение.

5. Центральный пучок– это множество прямых, проходящих через одну точку М ( х 1, у 1), называемую центром пучка. Каждая из прямых пучка описывается уравнением пучка у – у 1= к ( х – х 1) ( параметр пучка к для каждой прямой свой).

Все прямые пучка можно представить уравнением: l ( y – y 1) = m ( x – x 1), где l, m – не равные одновременно нулю произвольные числа.

Если две прямые пучка L 1и L 2соответственно имеют вид ( А 1 х + В 1 у + С 1) = 0 и ( А 2 х + В 2 у + С 2) = 0, то уравнение пучка: m 1( А 1 х + В 1 у + С 1) + m 2( А 2 х + В 2 у + С 2) = 0. Если прямые L 1и L 2пересекающиеся, то пучок центральный, если прямые параллельны, то и пучок параллельный.

6. Пусть даны точка М ( х 1, у 1) и прямая, заданная уравнением Ах + Ву + С = 0 . Расстояние d отэтой точки М до прямой: