Аурика Луковкина - Высшая математика. Шпаргалка
- Название:Высшая математика. Шпаргалка
- Автор:
- Жанр:
- Издательство:Array Литагент «Научная книга»
- Год:2009
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Аурика Луковкина - Высшая математика. Шпаргалка краткое содержание
Высшая математика. Шпаргалка - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Две матрицы А и В называются равными, если их размер одинаков и a ij = b ij . Нулевая матрица– это матрица, у которой все элементы равны нулю.
Единичной матрицейназывается квадратная матрица:

Матрицей, транспонированнойк матрице А размерности m х n называется матрица А тразмерности n х m , полученная из матрицы А если ее строки записать в столбцы а столбцы – строки.
Матрицы одинакового размера (однотипные)можно складывать, вычитать, перемножать и умножать на число.
Суммой (разностью)двух однотипных матриц А и В называется матрица С , элементы которой равны сумме или разности c ij = a ij ± b ij . При сложении справедливы:
А + В = В + А, (А + В) + С = А + (В + С), А + 0 = А .
Произведением матрицы А на число р называется матрица, элементы которой равны рa ij .
Справедливы свойства:
α ( βA ) = ( αβ ) А ;
( А + В ) α = αА + αВ ;
( α + β ) А = αА + βА .
Произведениемдвух квадратных матриц А и В называется матрица С , элемент которой, находящийся на пересечении i –ой строки и k –го столбца, является суммой парных произведений элементов i –ой строки первой матрицы на элемент k –ой строки второй матрицы С = АВ . То же правило распространяется на умножение прямоугольных матриц, у которых число столбцов матрицы–множимого равно числу строк матрицы–множителя.
Матрицы, для которых АВ = ВА , называются коммутирующими.
Справедливы свойства:
1) ЕА = АЕ = А ;
2) А ( ВС ) = ( АВ ) С ;
3) a( АВ ) = (a А ) В = А (a В );
4) ( А 1+ А 2) В = А 1 В + А 2 В, А ( В 1+ В 2) = АВ 1+ АВ 2;
5) А 0 = 0 А = 0;
6) ( АВ ) т= А т В т.
При умножении двух ненулевых матриц может получиться нулевая матрица.
8. Определители. Обратная матрица. Вырожденная и невырожденная матрицы. Система линейных уравнений
Определителем второго порядка,соответствующим матрице 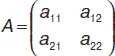 , называется число, равное
, называется число, равное
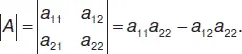
Свойства определителя:
1) величина определителя не меняется, если заменить его строки соответствующими столбцами или если к элементам какой–либо его строки или столбца прибавить соответствующие элементы другой строки или столбца, умноженные на одно и тоже число;
2) определитель поменяет знак при перемене мест его строк или столбцов;
3) определитель будет равен нулю, если элементы какого–либо столбца (или строки) равны нулю или элементы двух строк (или столбцов) соответственно равны.
Минором M ik элемента a ik определителя I А I называется определитель полученный из А вычеркиванием той строки и того столбца которым принадлежит этот элемент.
Алгебраическим дополнением A ik элемента a определителя | A | называется его минор, взятый со знаком (–1) i+k , A = (–1) i+ kM ik .
Определителем n– порядка,соответствующим квадратной матрице n –го порядка, называется число, равное сумме парных произведений элементов какой–либо строки (столбца) на их алгебраические дополнения.
Теорема.Если А и В – квадратные матрицы одного порядка с определителями | A | и | B |, то определитель матрицы С = АВ равен: | C | = | A | | B |.
Обратной матрицейдля квадратной матрицы А называется матрица А –1, которая удовлетворяет условиям АА –1 = А –1 А = Е . Матрица А называется вырожденной, если ее определитель | A | равен нулю.
Теорема.Матрица

где A ik – алгебраическое дополнение элемента a ik невырожденной матрицы А , является обратной для А .
Пусть дана система n линейных уравнений с n неизвестными:
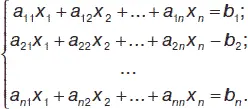
9. Числовые последовательности, арифметические действия над ними. Предел последовательности
Если каждому значению n из натурального ряда чисел – 1, 2, n – ставится в соответствие по определенному закону некоторое вещественное число а , то множество занумерованных вещественных чисел – а 1, а 2, а n – называется числовой последовательностью (последовательностью), числа а n называются элементамиили членамипоследовательности.
Числовая последовательность:
{ a n }, a n = f ( n ),
где n = 1, 2, 3… – номер члена последовательности.
Cпособы задания последовательностей:
1) аналитический (с помощью формулы n –члена);
2) рекуррентный (путем задания первого члена или нескольких членов и формулы для определения любого члена по известным членам);
3) словесный.
Суммой, разностью, произведениеми частным двух последовательностей{ x n } и { y n } называются соответственно следующие последовательности: { x n + y n }, { x n – y n }, { x n × y n }, { x n / y n }, в случае частного y n ≠ 0. Если в нуль обращается лишь конечное число членов последовательности знаменателя, то частное определяется с номера, отличного от нуля члена последовательности.
Последовательность называется возрастающей (убывающей), если для любого n выполняется условие: a n +1> a n ( a n +1< a n ). Возрастающие и убывающие последовательности называются строго монотонными.
Последовательность называется невозрастающей (неубывающей), если для любого n выполняется условие: a n +1≤ a n ( a n +1≥ a n ).
Невозрастающие и неубывающие последовательности называются монотонными.
Последовательность { a n } называется сходящейся, если существует такое число А , что для любого положительного числа ε > 0 найдется такой номер N , что при всех n > N | a n– A | < ε . Если последовательность не сходится, то она называется расходящейся.
Читать дальшеИнтервал:
Закладка:










