Аурика Луковкина - Высшая математика. Шпаргалка
- Название:Высшая математика. Шпаргалка
- Автор:
- Жанр:
- Издательство:Array Литагент «Научная книга»
- Год:2009
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Аурика Луковкина - Высшая математика. Шпаргалка краткое содержание
Высшая математика. Шпаргалка - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Число А называется пределом последовательности{ a n }, если для ε > 0 существует такое натуральное число N , что при всех n > N | a n– A | < ε . Обозначение предела последовательности: 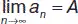 .
.
Теорема.Всякая сходящаяся последовательность имеет только один предел.
Для подпоследовательностей справедливо:
1) если последовательность сходится к пределу А , то и ее подпоследовательность сходится к пределу А ;
2) если все подпоследовательности некоторой последовательности сходятся, то все они сходятся к одному и тому же пределу и к нему же сходится исходная последовательность.
Теорема.Предел суммы (разности), произведения и частного равен сумме (разности), произведению и частному пределов, т. е., если 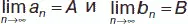 , то:
, то:
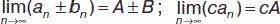 , где с – постоянная;
, где с – постоянная;
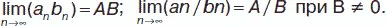
10. Ограниченные и неограниченные последовательности. Бесконечно большие и бесконечно малые последовательности
Последовательность { а n } называется ограниченной сверху (снизу), если существует число М ( m ) такое, что для любого n a n ≤ M ( a n ≥ m ). Число М ( m ) называется верхней (нижней) границей последовательности { a n }.
Последовательность { а n } называется ограниченной, если она ограничена и сверху, и снизу.
Теорема.Последовательность { а n } ограничена тогда и только тогда, когда существует число r > 0 такое, что | a n | < r для всех n .
Теорема.Свойства ограниченности последовательности сверху, снизу и с двух сторон не нарушатся при отбрасывании (добавлении) конечного числа членов последовательности.
Теорема.Сумма двух ограниченных последовательностей есть ограниченная последовательность.
Последовательность { а n } называется бесконечно малой, если для любого положительного ε существует такой номер N , что, начиная с него, для всех членов последовательности справедливо | a n | < ε .
Последовательность { а n } называется бесконечно большой, если для любого положительного Р существует такой номер N , что, начиная с него, для всех членов последовательности справедливо | a n | < Р .
Предел бесконечно большой последовательности при n > ∞ равен ∞.
Бесконечно большая последовательность не ограничена и, следовательно, расходится.
Теорема о связи бесконечно большой и бесконечно малой последовательностей.Для того чтобы последовательность { а n } была бесконечно большой, необходимо и достаточно, чтобы последовательность { b n } b n = 1 / а n была бесконечно малой.
Теорема.Если { а n } – бесконечно большая последовательность, а { b n } – сходящаяся последовательность, не являющаяся бесконечно малой, то их произведение есть бесконечно большая последовательность.
Свойства бесконечно малых последовательностей:
1) предел бесконечно малой последовательности равен нулю: 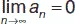 ;
;
2) стационарная последовательность с, с , …, с , … является бесконечно малой тогда, когда с = 0;
3) свойство последовательности быть бесконечно малой не нарушится, если отбросить (прибавить) конечное число членов;
4) пусть { b n } – бесконечно малая последовательность и для всех n справедливо а n ≤ b n , тогда последовательность { а n } тоже является бесконечно малой;
5) бесконечно малая последовательность ограниченна;
6) сумма (разность) двух бесконечно малых последовательностей есть бесконечно малая последовательность;
7) пусть { а n } – бесконечно малая последовательность, { b n } – ограниченная последовательность, тогда их произведение есть бесконечно малая последовательность;
8) пусть { а n } – бесконечно малая последовательность, а с – любое действительное число, тогда последовательность { са n } тоже бесконечно мала;
9) произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
11. Сходящиеся и расходящиеся последовательности. Предел последовательности
Последовательность { а n } называется сходящейся, если существует такое вещественное число А , что последовательность { а n– А } является бесконечно малой. Число А будет пределом последовательности: 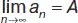 .
.
Сходящуюся последовательность можно представить в виде { a n } = { A + γ n }, где { γ n } – бесконечно малая последовательность.
Бесконечно малые последовательности являются сходящимися с пределом, равным нулю, бесконечно большие – расходящимися(сходящимися к бесконечности).
Точка бесконечной прямой называется предельной точкой последовательности, если в любой ее ε –окрестности содержится бесконечно много элементов данной последовательности.
Лемма.Каждая сходящаяся последовательность имеет только одну предельную точку, совпадающую с ее пределом.
Основные свойства сходящихся последовательностей:
1) всякая сходящаяся последовательность имеет один предел;
2) сходящаяся последовательность { a n } ограниченна;
3) пусть последовательности { a n } и { b n } сходятся и 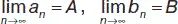 , тогда сходятся и последовательности { cx n } ( c = const) { a n ± b n } { a n × b n } { a n/ b n } (в случае частного B ≠ 0, b n ≠ 0, n = 1, 2, …). И их пределы вычисляются по общим правилам.
, тогда сходятся и последовательности { cx n } ( c = const) { a n ± b n } { a n × b n } { a n/ b n } (в случае частного B ≠ 0, b n ≠ 0, n = 1, 2, …). И их пределы вычисляются по общим правилам.
Теорема сравнения (предельный переход в неравенствах).Пусть заданы последовательности { a n }, { b n }. Тогда если последовательности { a n }, { b n } таковы, что a n ≤ (≥) b n , то 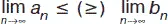 (данное утверждение неверно для строгих неравенств).
(данное утверждение неверно для строгих неравенств).
Теорема (принцип двустороннего ограничения).Пусть заданы последовательности { a n }, { b n }, { c n }. Тогда если a n ≤ b n ≤ c n и последовательности { a n } и { c n } сходятся к одному и тому же пределу В , то последовательность { b n } тоже сходится к тому же пределу: 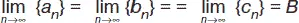 .
.
Интервал:
Закладка:










