Аурика Луковкина - Высшая математика. Шпаргалка

Следствия:

1) если все члены сходящейся последовательности { a n } не отрицательны (не положительны), то предел последовательности есть число неотрицательное (неположительное), ;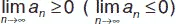

2) если все элементы сходящейся последовательности { a n } находятся на отрезке [ a, b ], то и предел этой последовательности { a n } лежит на данном отрезке, ;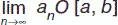

3) если все члены сходящейся последовательности { a n } a n ≤ ( і ) В, то 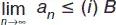, где В – некоторое число.

Теорема о сходимости монотонной ограниченной последовательности.Всякая неубывающая (невозрастающая) последовательность { a n }, ограниченная сверху (снизу) сходится. Иначе для того чтобы монотонная последовательность сходилась необходимо и достаточно, чтобы она была ограниченна.

Числовым рядомназывается выражение 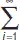a i = а 1+ а 2+…+ а n +…, где a i ( i = 1, 2…, n …) – вещественные или комплексные числа.

Частичной суммой ряда( n –ой частичной суммой) называется число S n = а 1+ а 2+…+ а n = 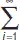a i .

Из частичных сумм можно образовать последовательность S 1= a 1, S 2= a 1+ a 2, S 3= a 1+ a 2+ a 3и т. д. Если существует предел последовательности частичных сумм ряда, то ряд называется сходящимся, а сам предел называется суммой ряда, обозначается 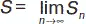. Если такового предела не существует, то ряд называется расходящимся.

Теорема.На сходимость ряда не влияет отбрасывание конечного числа его членов. Если ряд сходится, то его n –ый член стремится к нулю при неограниченном возрастании n , т. е. 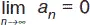. Пусть даны два ряда a n и b n . Тогда в результате сложения этих двух рядов получится ряд ( a n + b n ), при умножении получается ряд 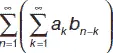, произведением ряда a n на число с будет ряд ca n ( с – вещественное или комплексное число).

Теорема.Пусть даны два ряда, имеющие соответствующие суммы a n = S 1и b n = S 2. Тогда справедливо: ( a n + b n ) = S 1+ S 2, 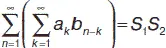, ca n = cS 1(где с – число).

Теорема (принцип сравнения).Пусть даны два ряда с положительными членами a n и b n . Если ряд a n сходится и a i ≥ b i ( i = 1, 2…, n ), то и ряд b n b n сходится, причем a n ≥ b n .

Теорема.Если члены ряда 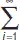a i не меньше соответствующих членов расходящегося ряда b n , то и ряд a n расходится.

Знакопеременный ряд– это ряд с произвольными вещественными числами.

Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов.

Знакопеременный ряд называется условно сходящимся, если он сходится, а ряд, составленный из абсолютных величин его членов, расходится.

Теорема.Всякий абсолютно сходящийся знакопеременный ряд есть ряд сходящийся.

Теорема.Если знакопеременный ряд сходится абсолютно, то он остается абсолютно сходящимся при любой перестановке его членов. При этом сумма ряда не зависит от порядка его членов.

Теорема.Если знакопеременный ряд сходится условно, то какое бы ни задали число А , можно так переставить члены этого ряда, чтобы его сумма в точности оказалась бы равной А . Кроме этого, можно так переставить члены условно сходящегося ряда, что после перестановки ряд окажется расходящимся.

Ряд с вещественными членами называется знакочередующимся, если два любых его соседних члена имеют разные знаки. Его иногда записывают следующим образом: (–1) n +1 a n ( a i > 0).

Теорема (признак сходимости Лейбница).Если члены знакочередующегося ряда a n удовлетворяют условиям | a n | > | a n +1 | ( n = 1, 2…) и 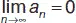, то ряд сходится. При этом если a n = S , то .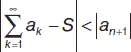

Ряд u n ( x ) называется функциональным, если его члены являются функциями действительной переменной х .

Областью сходимостифункционального ряда называется совокупность тех значений х , при которых функциональный ряд сходится. Если функциональный ряд сходится при х = х 0, то х 0называется точкой сходимости. Если ряд сходится в каждой точке некоторого множества, то говорят, что ряд сходится на этом множестве.