Аурика Луковкина - Высшая математика. Шпаргалка
- Название:Высшая математика. Шпаргалка
- Автор:
- Жанр:
- Издательство:Array Литагент «Научная книга»
- Год:2009
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Аурика Луковкина - Высшая математика. Шпаргалка краткое содержание
Высшая математика. Шпаргалка - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Общее уравнение плоскости: Ах + Ву + Сz + D = 0. Если А, В, С, D не равны нулю, то уравнение называется полным.
При D = 0 уравнение Ах + Ву + Сz = 0 определяет плоскость, проходящую через начало координат.
Если А = 0, то уравнение определяет плоскость, параллельную оси Ох . Если два из коэффициентов А, В, С равны нулю одновременно, то уравнение определяет плоскость, параллельную одной из координатных плоскостей: при А = 0 и В = 0 параллельно плоскости хОу , при А = 0 и С = 0 параллельно хОz , при В = 0 и С = 0 параллельно yOz . Уравнение Cz = 0 определяет плоскость xOy, By = 0 – плоскость xOz, Ax = 0 – плоскость yOz . Уравнение плоскости в «отрезках»: х / а + у / b + z / c = 1. Расстояние от точки М ( х 1, у 1, z 1) до плоскости:
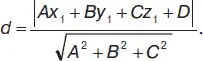
Пусть имеются две плоскости А 1 х + В 1 у + С 1 z + D 1= 0 и А 2 х + В 2 у + С 2 z + D 2= 0. Угол φ между этими плоскостями:
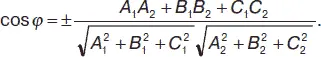
Условие равенства двух плоскостей: А 1 / А 2= В 1 / В 2= С 1 / С 2= D 1 / D 2. Условие параллельности плоскостей: А 1/ А 2= В 1/ В 2= С 1/ С 2. Условие перпендикулярности плоскостей: А 1 А 2+ В 1 В 2+ С 1 С 2= 0. Уравнение плоскости, проходящей через заданную точку М ( х 1, у 1, z 1) параллельно плоскости, заданной уравнением Ах + Ву + Сz + D = 0: А ( х – x 1) + В ( у – y 1) + С ( z – z 1) + D = 0. Уравнение плоскости, проходящей через три точки М 1( х 1, у 1, z 1), М 2( х 2, у 2, z 2), М 3( х 3, у 3, z 3):
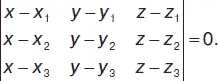
Уравнение плоскости, проходящей через две точки М 1( х 1, у 1, z 1) и М 2( х 2, у 2, z 2) перпендикулярно к плоскости, заданной уравнением A x + B y + C z + D = 0:
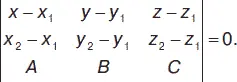
Уравнение плоскости, проходящей через точку М 1( х 1, у 1, z 1) перпендикулярно двум непараллельным плоскостям А 1 х + В 1 у + С 1 z + D 1= 0 и А 2 х + В 2 у + С 2 z + D 2= 0, имеет вид:
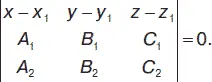
Имеем три плоскости, заданные общими уравнениями:
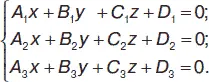
6. Прямая в пространстве
Всякая прямая определяется в пространстве системой двух уравнений
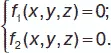
Канонические (симметричные) уравнения прямой:( x – x 0) / m = ( y – y 0) / p = ( z – z 0) / q , прямая проходит через точку M 0( x 0, y 0, z 0). Угол φ между двумя прямыми, заданными каноническими уравнениями:
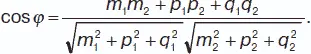
Условие параллельности двух прямых: m 1 / m 2= p 1 / p 2= q 1 / q 2. Условие перпендикулярности двух прямых: m 1 m 2+ p 1 p 2+ q 1 q 2= 0.
Пусть имеются прямая ( x – x 0) / m = ( y – y 0) / p = ( z – z 0) / q и плоскость Ах + Ву + Сz + D = 0. Условие параллельности прямой и плоскости: Am + Bp + Cq = 0. Условие перпендикулярности прямой и плоскости: A / m = B / p = C / q . Условие принадлежности прямой плоскости:
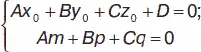
Если прямая задана параметрически x = x 0+ mt, y = y 0+ pt, z = z 0+ qt , то координаты точки пересечения этой прямой и плоскости Ах + Ву + Сz + D = 0 определяются по параметрическим уравнениям прямой при подстановке значений t , определенных ( Am + Bp + Cq ) t + Ax 0+ By 0+ Cz 0+ D = 0. Уравнение прямой, проходящей через точки М 1( х 1, у 1, z 1) и М 2( х 2, у 2, z 2):( х – х 1) / ( х 2– х 1) = ( у – у 1) / ( у 2– у 1) = ( z – z 1) / ( z 2– z 1). Уравнение плоскости, проходящей через точку М 0( х 0, у 0, z 0) перпендикулярно прямой ( x – x 1) / m = ( y – y 1) / p = ( z – z 1) / q , имеет вид: m ( x – x 0) + p ( y – y 0) + q ( z – z 0) = 0. Уравнение прямой, проходящей через точку М 0( х 0, у 0, z 0) перпендикулярно плоскости Ах + Ву + Сz + D = 0, имеет вид: ( х – х 0) / А = ( у – у 0) / В = ( z – z 0) / C . Уравнение плоскости, проходящей через М 0( х 0, у 0, z 0) и ( x – x 1) / m = ( y – y 1) / p = ( z – z 1) / q , не проходящую через М 0:
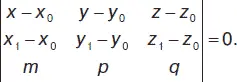
Уравнение плоскости, проходящей через М 0( х 0, у 0, z 0) и параллельной двум прямым:
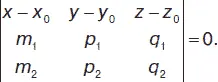
Уравнение плоскости, проходящей через ( x – x 1) / m 1= ( y – у 1) / p 1= ( z – z 1) / q 1и параллельной ( x – x 2) / m 2= ( y – y 2) / р 2= ( z – z 2) / q 2имеет вид:
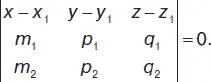
Уравнение плоскости, проходящей через ( x – x 1) / m 1= ( y – y 1) / p 1= ( z – z 1) / q 1перпендикулярно Ах + Ву + Сz + D = 0;
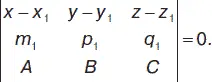
7. Матрицы и действия над ними
Матрицейразмерности m x n называется прямоугольная таблица вида:
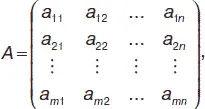
или А = ( a ij ), где i = 1, 2…, m; j = 1, 2…, n . Числа a ij – называются элементами матрицы. Если m = 1, а n > 1, то матрица является матрицей–строкой. Если m > 1, а n = 1, то матрица является матрицей–столбцом. Если m = n , то матрица называется квадратной, а число ее строк (или столбцов) называется порядком матрицы.
Читать дальшеИнтервал:
Закладка:










