Сергей Струговец - Естественная механика природы. Автореферат книги

Чтобы определить связь силы гравитационного взаимодействия тел с их массой, необходимо и достаточно установить функциональную зависимость между количеством КУ, составляющих тела, и количеством КС, эти тела соединяющих.

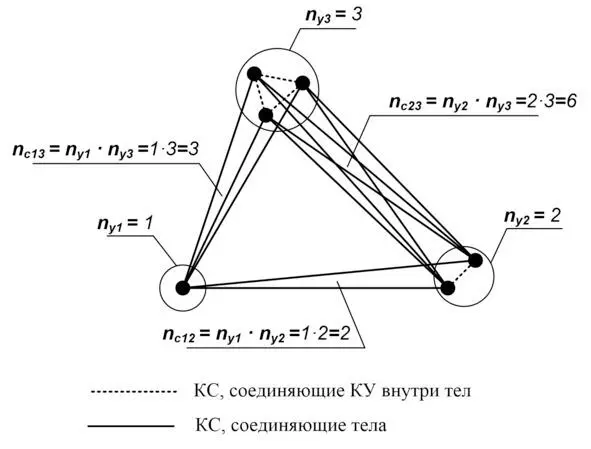
Модель элемента структуры нашей Вселенной, наглядно показывающая зависимость количества КС, соединяющих частицы вещества, от произведения количества КУ, входящих в эти частицы (наглядное объяснение причины произведения инертных масс в законе тяготения).

На рисунке показано, что для любых двух материальных тел в нашей Вселенной, состоящих из, соответственно, n у1 и n у2 узловых квантов, количество соединяющих эти два тела КС ( n c12 ) всегда равно:

Поэтому сила гравитации ( F g ), действующая между двумя телами, расположенными достаточно далеко друг от друга, равна:

где F cg – примерно одинаковая (средняя) сила гравитационного взаимодействия, которую создаёт ГСЛ каждого из связывающих тела соединяющих квантов.

Учитывая связь количества КУ в телах с массой каждого из них ( m у ) и с массой самих тел ( m 1 и m 2 ), получаем:

Отсюда:

Примечание. В формуле F g= G m 1m 2/r 2 , предложенной Ньютоном, произведение масс частиц вещества присутствует явно, а постоянная величина 1 / m у 2 скрыта в коэффициенте G , называемом гравитационной постоянной. То есть хорошо объясняется не только произведение масс в числителе формулы, но и, частично, размерность G (кг 2в знаменателе размерности этого коэффициента, в СИ). Ну, а то, что F cg обратно пропорциональна r 2 – это общий закон для обеих силовых линий соединяющего кванта. Кстати сказать, постулировав несколько иначе понятие «скорость», можно считать, что F cg обратно пропорциональна r 3 . Такая зависимость, как это будет показано ниже, используется в СКТВ для объяснения причин изменения размеров нашей Вселенной по закону Хаббла.

Таким образом, термин «тяжёлая масса» утрачивает свой физический смысл, так как никакой прямой причинно-следственной связи между массой и силой гравитации нет. Размерность «тяжёлой» массы в формуле закона тяготения сокращается, а в размерности силы масса присутствует, согласно второму закону Ньютона, только как инертная. Соответственно, теряет всякий смысл и сложнейший математический аппарат общей теории относительности Эйнштейна, описывающий, как тяжёлая масса искривляет континуум пространства-времени, создавая этим гравитацию.

Итак, гравитацию СКТВ объясняет настолько просто и точно, что сомневаться в правильности такого объяснения, на мой взгляд, невозможно. Но это объяснение справедливо, только если всё вещество нашей Вселенной состоит, как это следует из СКТВ, из точечных элементов с одинаковой постоянной массой, каждый из которых притягивается к каждому другому посредством одинаковых силовых связей. Неважно даже как эти связи интерпретировать, как конкретные линии одномерной материи или как некие наглядно-непредставимые поля. Поэтому закон всемирного тяготения – это, в свою очередь, прямое экспериментальное доказательство соответствия СКТВ объективной реальности.

Следует также отметить, что наблюдаемое отсутствие эффекта экранирования гравитации веществом исключает возможность существования в природе гравитационного излучения. Без экспериментального опровержения отсутствия этого эффекта, любые данные, истолкованные, как проявление гравитационного излучения (включая данные об обнаружении гравитационных волн), нельзя рассматривать как доказательство его существования.

Примечание. Гравитационные силовые линии, соединяющие наблюдателя с вращающимся веществом (от массивных космических объектов до вращающихся вокруг атомных ядер электронов и КУ в самих ядрах), действуют на него, как шатуны кривошипно-шатунных механизмов, только не жёсткие, а упругие. Возникающие вследствие этого колебания могут создать иллюзию наблюдения волн гравитационного излучения. Но это не более чем иллюзия.

На приведённом ниже рисунке изображено, по сути, то же самое, что и на предыдущем, но узловые кванты показаны со знаками их полярности, а вместо гравитационных силовых линий используются спаренные с ними ЭСЛ.

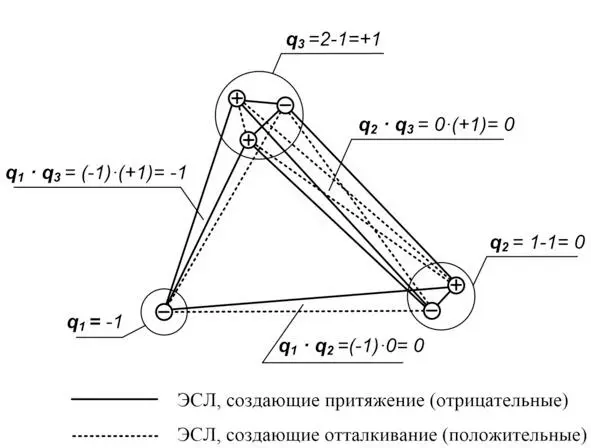
Модель элемента структуры нашей Вселенной, наглядно показывающая, что произведение электрических зарядов в числителе закона Кулона, является следствием разницы в количестве КС, создающих противоположное по направлению электрическое взаимодействие между соединяемыми ими телами.

Количество узловых квантов в составе материального тела, имеющих положительную полярность, обозначим n у+ , а отрицательную, соответственно, n у—. Разница между количеством узловых квантов с положительной и отрицательной полярностью и определяет в структурно-квантовой теории понятие электрический заряд материального тела ( q ), включая его знак:

То есть, электрический заряд в СКТВ – это безразмерная величина, это разница в количестве узловых квантов противоположной полярности в составе частицы вещества, и только.Изображённая на рисунке схема показывает, что сила электрического взаимодействия между двумя телами ( F е ) связана не с их электрическими зарядами, как таковыми ( q 1 и q 2 ), а с силами ( F се ), которые создают ЭСЛ каждого из КС, соединяющих эти тела, и разницей в количестве соединяющих квантов, создающих электрические силы противоположной направленности. Хорошо видно, что указанная разница в количестве КС, имеющих электрические силы противоположной направленности, прямо пропорциональна произведению электрических зарядов взаимодействующих тел.Если принять, что силы электрического взаимодействия между входящими в состав частиц вещества узловыми квантами ( F се ) по абсолютной величине в среднем одинаковы, мы получим: