Джеймс Гордон - Конструкции, или почему не ломаются вещи

Увеличение числа канатов и тросов в конструкциях судов, бипланов (а также палаток) приводит обычно к экономии веса [112] Вес конструкции, состоящей из n параллельных элементов и имеющей общую длину L , которая должна выдерживать заданную растягивающую нагрузку Р , выражается следующим образом: где Z - полный вес всех п элементов на единицу длины; s - допустимое напряжение; k - коэффициент, связанный с изобретательностью конструктора; W - работа разрушения материала; ρ - плотность материала. Вывод этой формулы можно найти в книге Кокса ( Сох Н. L. The Design of Structures of Least Weight.- 1965), я лишь слегка ее модифицировал. . Но за это приходится платить повышением лобового сопротивления, общим усложнением конструкции и высокой стоимостью ее эксплуатации. Похожий принцип можно встретить и в животном мире, где природа не скупилась на детали, например мышцы и сухожилия, работающие на растяжение. Для уменьшения веса законцовок она использовала тот же принцип, что и моряки елизаветинских времен. Концы многих сухожилий разветвляются в некоторую веерообразную конструкцию, которую Френсис Дрейк назвал бы "птичьей лапой". Каждая веточка сухожилия имеет отдельное крепление к кости. Так минимизируется вес (и, возможно, метаболическая стоимость).

Мы уже говорили в предыдущей главе, что для ряда материалов величины прочности на сжатие и растяжение часто сильно различаются, но для многих весьма распространенных материалов, таких, как сталь, это различие не очень велико, так что массы коротких растянутых и сжатых элементов должны быть более или менее одинаковыми. На самом деле сжатый короткий стержень может быть даже легче растянутого, так как для него иногда не нужны законцовки, совершенно необходимые в случае растяжения.

Однако с увеличением длины такого стержня дает себя знать эйлерова потеря устойчивости. Напомним, что критическая нагрузка, при которой сжатый стержень длиной L начинает выпучиваться, изменяется пропорционально 1/L 2 . Это означает, что для стержня с заданным поперечным сечением предельное напряжение при сжатии с увеличением L убывает очень быстро. Чтобы выдержать заданную нагрузку, длинный стержень должен быть гораздо толще и, следовательно, тяжелее короткого. Как мы установили в предыдущем параграфе, в случае растяжения все происходит как раз наоборот.

Очень поучительно сравнить, как конструкционный элемент длиной 10 м выдерживает нагрузку весом 1 т (10 4Н) в условиях растяжения и сжатия.

Растяжение.Для стального троса допустимое напряжение примем равным 350 МН/м 2(35 кгс/мм 2). Принимая во внимание крепления на его концах, найдем общий вес конструкции равным примерно 3,5 кг.

Сжатие.Попытаться удержать нагрузку в 1 т (10 4Н) с помощью одного сплошного стального стержня длиной 10 м было бы просто глупо: чтобы избежать потери устойчивости, его пришлось бы сделать очень толстым и, следовательно, очень тяжелым. На практике можно, например, использовать стальную трубу диаметром около 16 см с толщиной стенок около 5 мм. Такая труба будет весить около 200 кг. Другими словами, ее вес будет в 50-60 раз больше, чем у стального стержня, работающего в тех же условиях на растяжение. Стоимость конструкции увеличится примерно в той же пропорции. Далее, если мы захотим распределить нагрузку между несколькими деталями, то ситуация не только не станет лучше, а значительно ухудшится. Если мы попробуем держать нагрузку в 1 т не с помощью одной колонны, а, скажем, с помощью похожей на стол конструкции на четырех стержнях 10-метровой высоты, то общий их вес удвоится и достигнет 400 кг. Чем на большее число элементов мы распределим данную нагрузку, тем больше будет вес всей конструкции: он растет как n 1/2, где n- число элементов (см. приложение 4).

С другой стороны, если мы будем увеличивать нагрузку при фиксированной длине, то ситуация в случае сжатой конструкции будет выглядеть получше. Например, если увеличить нагрузку в сто раз, с 1 т до 100 т, то, если вес растянутой конструкции увеличится соответственно с 3,5 до 350 кг, вес одной колонны высотой в 10 м увеличится только десятикратно, с 200 до 2000 кг. Поэтому в случае сжатия гораздо экономичнее поддерживать большую нагрузку, чем малую (рис. 152). Все эти рассуждения справедливы также и для панелей, пластин и оболочек (см. приложение 4).

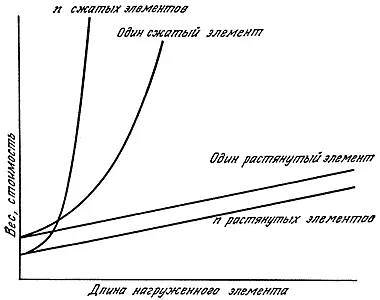
Рис. 152. Зависимость относительного веса (и стоимости) детали, которая должна передать заданную нагрузку, от ее длины.

Приведенный анализ подтверждает рациональность таких конструкций, как палатки и парусные суда. В них сжимающие нагрузки действуют концентрированно на небольшое количество по возможности коротких мачт или шестов. В то же время растягивающие нагрузки, как мы уже говорили, лучше распределить среди большого количества канатов и тросов. Поэтому шатер, имеющий единственный шест и множество растяжек, является самым легким "зданием", которое только можно построить при заданном объеме. Любая палатка будет легче и дешевле капитального здания из дерева или камня. Точно так же катер или шлюп с единственной мачтой имеет более легкую и эффективную оснастку, чем шхуна, кеч или любой более сложный корабль с большим количеством мачт. Именно поэтому были тяжелы и неэффективны А-образные или треугольные мачты древних египтян и конструкторов викторианских броненосцев (см. гл. 10).

Конструкция человеческого тела имеет много общего с конструкцией шатра и парусного корабля. Небольшое количество сжатых деталей, то есть костей, расположенных примерно в центре конструкции, окружено множеством мышц, сухожилий и связок, работающих на растяжение, причем эта система гораздо сложнее системы парусов и канатов полностью оснащенного корабля. Кстати, с конструкционной точки зрения две ноги лучше, чем четыре, а сороконожка может существовать только потому, что ноги у нее весьма коротки.

Напомним, что уже столетия назад Галилею пришла мысль о том, что, поскольку вес конструкции растет, как куб ее размеров, а поперечное сечение несущих деталей увеличивается пропорционально квадрату размеров, то напряжения в материале геометрически подобных конструкций должны расти пропорционально их размерам. Если разрушение конструкции происходит из-за растягивающих напряжений, прямо или косвенно определяемых ее собственным весом, то это означает, что с увеличением размеров относительная толщина и вес несущих деталей должны расти не пропорционально размерам и весу всей конструкции, а гораздо быстрее. Поэтому размеры таких конструкций не могут превышать некоторого предела.