Джеймс Гордон - Конструкции, или почему не ломаются вещи

Короче говоря, Ньютон был в немалой степени предрасположен к тому, чтобы питать отвращение к Гуку как к человеку и ко всему, что тот отстаивал, включая и теорию упругости. Так случилось, что после смерти Гука Ньютону довелось прожить еще 25 лет, и значительную часть этого времени он посвятил очернению памяти Гука и прикладных наук. А поскольку авторитет Ньютона в научном мире был непререкаем и его точка зрения совпадала с общественным настроением и интеллектуальными течениями того времени, такие дисциплины, как расчет конструкций, не обрели популярности в течение многих лет даже после смерти Ньютона.

Таким образом, в течение всего XVIII в. сохранялось такое положение, при котором, несмотря на то, что принцип сопротивления материалов был в самом общем виде объяснен Гуком, его труды и дела не имели последователей. При таком состоянии дел какие-либо расчеты для практических целей были едва ли возможны.

Следовательно, пользы от того, что существовали представления об упругости, для инженерных целей почти не было. Французские инженеры XVIII в. отдавали себе в этом отчет и с сожалением создавали конструкции (которые довольно часто разваливались) с помощью той теории, которая имелась в их распоряжении. Английские же инженеры, которые также понимали это, обычно были безразличны к "теории", и конструкции промышленной революции создавались кустарными методами. Они разрушались, может быть, чуть реже французских.

Кроме Ньютона и предрассудков XVIII в. главной причиной столь долгого застоя в теории упругости было то, что те немногие ученые, которые все же занимались атой проблемой, пытались анализировать силы и перемещения, рассматривая конструкцию целиком как это делал и Гук, - вместо того чтобы перейти, к силам и деформациям, которые существуют в каждой точке внутри материала. Предпринимавшиеся в XVIII и XIX вв. такими выдающимися умами, как Леонард Эйлер (1707-1783) и Томас Юнг (1773-1829), попытки решать вполне стандартные с сегодняшней точки зрения задачи кажутся современному инженеру невероятнейшими интеллектуальными ухищрениями.

Концепция упругости материала в точке сводится к понятию о напряжении и деформации, которое впервые в обобщенной форме было сформулировано Огюстом Коши (1789-1857) в его статье, направленной во Французскую академию наук в 1822 г. После работ Гука эта статья была, быть может, самым важным событием в истории развития теории упругости. После нее появилась надежда, что эта наука наконец станет орудием в руках инженеров, а не эмпиреями нескольких эксцентричных мыслителей. На портрете, написанном примерно в то же время, Коши выглядит довольно бойким молодым человеком; несомненно, в прикладной математике он был большой силой.

Когда в XIX в. английские инженеры наконец снизошли до того, чтобы познакомиться с работами Коши, то обнаружили, что, усвоив основные понятия о напряжениях и деформациях, можно сразу упростить все исследования по расчету конструкций. Сегодня эти понятия в широком ходу, и трудно объяснить то замешательство и смущение, которые иногда испытывают при упоминании о них неспециалисты. У меня как-то была аспирантка, незадолго до этого удачно защитившая диплом по биологии. Изучение понятий о напряжениях и деформациях вывело ее из душевного равновесия настолько, что она сбежала из университета и бесследно исчезла. Почему - я так и не пойму до сих пор.

Оказывается, к представлению о напряжении был очень близок еще Галилей. В "Двух новых науках" - книге, написанной им в старости в Арцетри, - он ясно указывает, что растягиваемый стержень имеет прочность, которая при постоянстве остальных условий пропорциональна площади его поперечного сечения. Иными словами, если стержень сечением 2 см 2разрывается при нагрузке 1000 кгс, то стержень сечением 4 см 2разрывается при нагрузке 2000 кгс. Кажется почти невероятным, что потребовалось почти два столетия, чтобы разделить разрушающую нагрузку на площадь поверхности в месте разрыва, дабы получить величину, называемую сегодня разрушающим напряжением (в упомянутом выше случае 500 кгс/см 2) и относящуюся ко всем стержням из того же материала.

Коши осознал, что такое представление о напряжении можно использовать не только для того, чтобы предсказать разрушение материала, но и для более общего описания состояния тела в любой его точке. Другими словами, напряжение в твердом теле напоминает давление в жидкости или газе. Оно является мерой воздействия внешних сил на атомы и молекулы, из которых состоит материал и которые вынуждены под действием этих сил сближаться или удаляться друг от друга.

Таким образом, сказать, что напряжение в данной точке какого-то куска стали составляет 500 кгс/см 2, ничуть не более вразумительно и не менее таинственно, чем сказать, что давление в шинах моего автомобиля 2 кгс/см 2. Однако, хотя понятия о давлении и напряжении вполне сопоставимы, нужно иметь в виду, что давление действует в любом направлении внутри жидкости, тогда как напряжение является величиной, характеризующейся определенными направлениями действия. Напряжение может, в частности, действовать в одном-единственном направлении; во всяком случае, пока мы будем считать, что это именно так.

В количественном выражении напряжение в заданной точке определяется отношением силы, или нагрузки, приходящейся на небольшую площадку в окрестности этой точки, к величине этой площадки [5] Здесь явная аналогия со скоростью движения, которая в каждый данный момент времени равна отношению пути, пройденного за малый отрезок времени, к величине этого отрезка времени. .

Если напряжение в некоторой точке мы обозначим буквой s , то напряжение = s = (нагрузка/площадь) = ( Р/А ),где Р - нагрузка, а А - площадь, на которую, как можно считать, эта нагрузка действует (рис. 6).

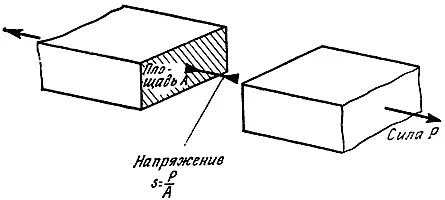
Рис. 6. Напряжение, возникающее в бруске при растяжении. (Ситуация при сжатии выглядит аналогичным образом.)

Вернемся теперь к нашему кирпичу, который в предыдущей главе мы оставили висящим на веревке. Если кирпич весит 5 кг, а веревка имеет сечение 2 мм 2, то кирпич натягивает веревку с силой 5 кгс, а напряжение в веревке s = (нагрузка/площадь) = ( Р/A ) = 5 кгс/2 мм 2= 2,5 кгс/мм 2,или, если угодно, 250 кгс/см 2.