Борис Штерн - Прорыв за край мира

Вход в стадию инфляции, как и в сценарии Гута, — термодинамический: горячая протовселенная расширяется и адиабатически охлаждается. Если в начале поле находится в термодинамическом равновесии при высокой температуре, оно должно «сесть» в нуль. Это довольно общее свойство систем — находиться при высокой температуре в наиболее симметричном состоянии (на самом деле изображенный потенциал похож на донышко бутылки в комплексных координатах, и нуль оказывается центром симметрии). При расширении зародыша вселенной опять происходит переохлаждение, и инфляция стартует точно так же, как изложено выше. И точно так же вселенная успевает раздуться на десятки порядков величины, пока поле, преодолевая вязкое трение, катится вниз с «пологой горки».

Разница в том, что в этом сценарии поле, не встречая никаких барьеров, в конце концов целиком сваливается в минимум. Потенциальная энергия поля превращается сначала в энергию его колебаний, а потом в конечном счете передается рождаемым частицам. Наступает новое термодинамическое равновесие, дальше всё идет по хорошо знакомому закону Фридмана, хотя впереди остается еще много нетривиальных событий.

Этот вариант выхода из инфляции пережил придирчивую проверку многими авторами — он действительно работает при достаточно общих предположениях.

Как в исходном сценарии Гута, так и в новом сценарии (он так и называется: «новая инфляция») остается один этап, который для своего объяснения требует слегка напрячься: как протовселенная добралась до старта инфляции? Она должна была достаточно расшириться и остыть, чтобы скалярное поле с отрицательным давлением перевесило энергию частиц и переменных полей. Дистанция от планковского состояния до начала раздувания относительно невелика, и проблема ее преодоления решается несравненно проще, чем создание огромной Вселенной без механизма инфляции. И всё же зазор в три порядка по температуре и интервал в миллион планковских времен требуется преодолеть (он именно таков, если механизм приводится в действие полем масштаба великого объе-динения).Вероятно, для описания этого скачка можно было бы использовать что-то вроде квантомеханического описания подбарьер-ного туннелирования (распад ядер и т.п.). Можно было бы… если б существовала наука под названием «квантовая гравитация». Увы, до применения квантовой механики к подобным задачам еще далеко. Но, по крайней мере, концепция туннельного перехода дает подходящую метафору (см. рис. 20.3), позволяющую легко смириться с проблемой доинфляционной стадии.

20.3. Микеланджело. Сотворение мира. Фрагмент

Следующий важный шаг сделал Андрей Линде уже без других претендентов на приоритет. На самом деле всё может быть еще проще — инфляция может произойти без всяких хитростей типа специального потенциала с плоским максимумом в нуле и без термодинамического равновесия с переохлаждением. Возьмем произвольное поле с естественным чашеобразным потенциалом.

Предположим, что вблизи планковского состояния образовался фрагмент пространства-времени, заполненного скалярным полем. «Вблизи» означает удаление от планковских условий, достаточное для того, чтобы фрагмент мог рассматриваться в рамках классической теории. Пусть поле будет достаточно однородным, а вклад горячей материи незначительным. Тогда давление в нем может оказаться отрицательным, удовлетворяющим условию инфляции: р < -1/3 ε .

Примет ли эта инфляция «вселенский» масштаб (т.е. раздует пространство на много порядков) или тут же прекратится? Это зависит от того, насколько пологий склон потенциала и насколько быстро пошло раздувание. Напомним: скорость раздувания (постоянная Хаббла) играет роль вязкого трения. Для большой скорости раздувания требуется большое отрицательное давление, значит, и большая плотность энергии, она же — потенциал поля на картинке ( V ( φ ) и ε в формуле совпадают, если поле однородно и постоянно). А для пологости склона ось X должна быть длинной, т.е. величина φ должна быть большой. Величина поля имеет размерность массы, и необходимое значение оказывается больше планковской массы. Ничего страшного, величина поля — достаточно абстрактная величина, главное, чтобы значение потенциала было ниже планковского масштаба — тогда есть классическое пространство-время, с которым можно работать. Еще важно, чтобы поле было достаточно однородным в некоторой области пространства, в несколько раз превышающей размеры горизонта.

21.1. Андрей Линде, 1989 год. Фото из архива А. Линде

Так вот, если «чаша» потенциала достаточно широка и если природа пробует любые стартовые условия, то она обязательно попробует и те, что перечислены выше. И тут уже возврата нет — готова гигантская вселенная. И не только… Но об этом «не только» — ниже Из-за того, что для запуска механизма достаточно подходящей комбинации из разнообразного множества случайных начальных условий, Андрей Линде назвал этот сценарий хаотической инфляцией. Только надо помнить, что термин «хаотический» относится лишь к старту. В дальнейшем всё происходит как и в предыдущем варианте — вполне регулярно и с предсказуемым исходом.

Большое преимущество этого сценария в том, что не требуется ни термодинамического равновесия, ни фазового перехода, предшествующих инфляции. В сценариях Гута и «новой инфляции» цепочка событий выглядела следующим образом: горячая вселенная — переохлаждение — инфляция — горячая вселенная. В случае с хаотической инфляцией первые две стадии, каковые, безусловно, являются обузой, отпадают. Не надо больше объяснять, как установилось доинфляцион-ное термодинамическое равновесие (далеко не очевидно, что это возможно), не нужен весьма специфический вид потенциала и т.п.

Пожалуй, хаотическая инфляция и есть общепринятая ныне концепция зарождения Вселенной, точнее, ее часть.

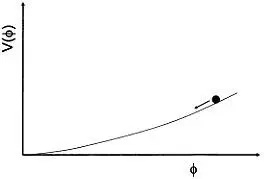
Рис. 21.2. Схема потенциала в концепции хаотической инфляции: поле находится на склоне потенциала, но скатывается настолько медленно, что пространство успевает раздуться на десятки порядков

В этот момент, прежде чем продолжать рассказ, стоит остановиться и задаться вопросом: а не потеряна ли у нас почва под ногами? Мы заглянули в такие дикие масштабы природы, которые невозможно ни представить, ни воспроизвести, — откуда у нас может быть уверенность, что наши методы познания работают и там? Не является ли всё вышеизложенное лишь буйной фантазией теоретиков, которую невозможно хоть как-то сопоставить с опытом?