Г. Гурев - Системы мира (от древних до Ньютона)

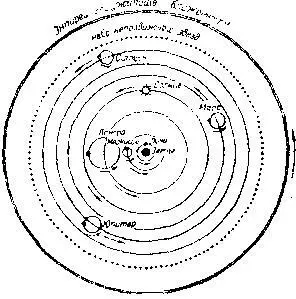
Фиг. 14. Птолемеевская система мира с главными эпициклами, по которым движутся планеты. Средневековые богословы за небом неподвижных звезд помещали эмпирей или «жилище блаженных» — местопребывание бога, ангелов и прочих «небожителей».

Он исходил из предположения, что чем медленнее движения планеты, тем дальше она от Земли, так что Луна должна находиться ближе всех к нам, а Сатурн — дальше всех. Что касается Солнца, то оно должно быть дальше от Земли, чем Луна, потому что движение его медленнее и Луна часто покрывает собой Солнце, вызывая этим солнечные затмения. Орбиты Меркурия и Венеры Птолемей принял внутри солнечной орбиты, орбиты же Марса, Юпитера и Сатурна — вне солнечной орбиты, потому что первые две планеты всегда видны близ Солнца, а другие удаляются от Солнца на большие расстояния. Подобное распределение планет он оправдывал еще тем, что всего «приличнее» принимать столько же небесных тел над Солнцем (Марс, Юпитер и Сатурн), сколько и под ним (Луна, Меркурий и Венера).

Как мы уже отметили, теория эпициклов, исходя из допущения равномерно — кругового движения небесных тел, стремится прежде всего объяснить особенности в движении планет. Она обращает внимание на то, что при движении по эпициклу и центра эпицикла по деференту, направление движения планеты должно меняться. В этих переменах она и видит объяснение всех кажущихся неправильностей в движении планет.

Когда движение планеты по эпициклу направлено в сторону движения центра эпицикла по деференту, наблюдателю с Земли должно казаться, что планета движется со скоростью равной сумме этих скоростей, так что в это время должно получиться прямое движение планеты. Наоборот, когда движения эпицикла и планеты направлены в прямо противоположные стороны, причем движение планеты по эпициклу быстрее движения центра эпицикла, наблюдателю с Земли должно казаться, что планета движется со скоростью, равной разности этих скоростей, и поэтому в это время планета будет казаться движущейся в обратном направлении. Наконец, в тех точках, где планета меняет направление своего движения, и скорость движения по эпициклу делается равной скорости движения центра эпицикла по деференту, планета с Земли должна некоторое время казаться остановившейся. После стояния планеты, видимая с Земли скорость ее движения по эпициклу превосходит скорость движения центра эпицикла, причем оба эти движения направлены в разные стороны, и наблюдателю с Земли кажется, что прямое движение планеты изменилось на обратное и что планета «завязала узел», описала петлю среди звезд.

Мы видим, таким образом, что при помощи теории эпициклов и деферентов удается объяснить второе неравенство в движении планет, т. е. прямые и попятные движения планет и их стояние. Но интересно, что одновременно представить правильно и направления с Земли планеты и расстояния планет от Земли одними и теми же эпициклами нельзя.

Чтобы положения планет, вычисленные на основании теории эпициклов, согласовались с наблюдаемыми положениями, необходимо было знать радиусы эпициклов и деферентов и скорости движения. С этой целью Пто- лемей принял, что в периодах времени обращения по этим кругам есть различие для трех «верхних», т. е. далеких планет (Марса, Юпитера и Сатурна) и для двух «нижних», т. е. близких (Меркурия и Венеры). Все верхние планеты совершают полный оборот по окружности эпицикла в одинаковый промежуток времени, равный году, т. е. периоду, в течение которого Солнце возвращается к одним и тем же звездам. Наоборот, у нижних планет период обращения по эпициклу различен и равен промежутку времени, в течение которого планета возвращается к прежним зоездам (Меркурий—88 дней, Венера — 225). Точно так же Птолемей определял различно промежуток времени, в течение которого центр эпицикла совершает полный оборот по окружности деферента. Он допускал, что для Марса, Юпитера и Сатурна этот промежуток различен и равен тем периодом времени, в течение которого каждая из этих планет, описав полную окружность на небосводе, возвращается к прежним звездам (Марс — почти 2 года, Юпитер—12 лет, Сатурн — почти 30 лет). Что же касается других двух планет, Меркурия и Венеры, которые видны лишь недалеко от Солнца, то для них, наоборот, этот промежуток Птолемей считал одинаковым и равным году.

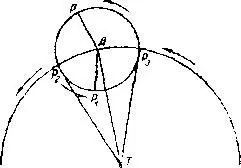
Фиг. 15. Видимое движение планеты по Птолемею. А — центр эпицикла, по которому равномерно движется планета в том же направлении, что и деферент, движущийся вокруг земли Т. Когда планета находится в точке Р, ее движение с Земли будет казаться прямым, ибо движения по эпициклу и деференту направлены в одну сторону. При положении Pj движение планеты из точки Т будет казаться обратным, ибо движение по эпициклу направлено в обратную сторону. При переходе от одного движения к другому, в точках Р ?и Р, планета будет казаться остановившейся.

По системе Птолемея Земля занимает несколько эксцентрическое положение внутри деферента, а все плоскости деферентов проходят через центр земного шара и наклонены друг к другу под различными углами, равно как н плоскости эпициклов к соответствующим деферентам. Дело в том, что наблюдения какой‑нибудь планеты, например Юпитера, показывают, что эта планета не движется в плоскости эклиптики (т. е. того круга, по которому, нам кажется, движется Солнце), а бывает то к северу, то к югу от этого круга. Чтобы учесть это обстоятельство, Птолемей принял, что плоскости тех кругов, которые служат для объяснения видимого движения Юпитера и других планет, не совпадают с плоскостью круговой орбиты Солнца, а несколько наклонены к ней. Следовательно, чтобы на основании теории эпициклов воспроизвести движение какой- нибудь планеты со всеми ее петлями, надо не только подобрать соответствующим образом скорости движения планеты и центра эпицикла (т. е. радиусы деферента и эпицикла и времена обращения центра эпицикла по деференту и планеты по эпициклу), но и углы наклона плоскостей деферента и эпицикла к эклиптике.

Итак, в движении планет были замечены некоторые особенности, для объяснения которых Птолемею приходилось плоскость каждого эпицикла наклонять под различными углами как к плоскостям остальных эпициклов, так и к плоскости деферента. Таким образом получилась весьма сложная система взаимно наклоненных круто в. А если мы к тому же примем во внимание, что вследствие крайней сложности закона изменения скорости видимого движения планет, для каждой из планет пришлось ввести целый ряд эпициклов, то станет ясно, какой громоздкой и запутанной была птолемеева система мира.