Брайан Грин - Элегантная вселенная (суперструны, скрытые размерности и поиски окончательной теории)

Но так же, как дети смогут начать покидать подвал, как только номинал бросаемых им денег станет достаточно большим, электроны начнут вырываться с поверхности металла, как только частота падающего на них света — его энергетический номинал — станет достаточно высокой. Далее, так же, как в случае, когда владелец однодолларовых купюр увеличил общую сумму сбрасываемых денег, увеличив число бросаемых банкнот, интенсивность луча света, имеющего заданную частоту, возрастет при увеличении числа фотонов, которые он содержит. И точно так же, как большее число долларов приведет к тому, что больше детей смогут покинуть подвал, увеличение числа фотонов приведет к тому, что большее число электронов испытает соударение и покинет металл. Обратите внимание, что энергия каждого из этих электронов после выхода из металла зависит исключительно от частоты светового луча, а не от его суммарной интенсивности. Так же, как дети покидают подвал с 15 центами, независимо от того, сколько купюр было брошено им с балкона, каждый электрон покидает поверхность с одной и той же энергией и, следовательно, с одной и той же скоростью, независимо от общей интенсивности падающего света. Большее количество денег просто означает, что большее число детей смогут покинуть подвал; большая суммарная энергия светового луча означает, что больше электронов будет вырвано из металла. Если мы хотим, чтобы дети покидали подвал с большим количеством денег, мы должны увеличить номинал купюр, которые им бросаем; если мы хотим, чтобы электроны выходили из металла с большей скоростью, следует увеличить частоту падающего светового луча, т. е. увеличить энергетический номинал фотонов, которые падают на поверхность металла.

Сказанное полностью подтверждается экспериментальными данными. Частота света (его цвет) определяет скорость вылетающих электронов, суммарная интенсивность света — количество вылетевших электронов. Таким образом, Эйнштейн показал, что гипотеза Планка о дискретности энергии на самом деле отражает фундаментальное свойство электромагнитных волн: они состоят из частиц — фотонов, которые представляют собой маленькие порции или кванты света. Дискретность энергии, заключенной в таких волнах, связана с тем, что они состоят из дискретных объектов.

Прозрение Эйнштейна представляло собой большой шаг вперед. Но, как мы увидим ниже, история была не такой гладкой, как может показаться.

Каждому известно, что вода (и, следовательно, волны на поверхности воды) состоит из огромного количества молекул. Поэтому так ли удивительно, что световые волны тоже состоят из огромного числа частиц — фотонов? Удивительно. Но главный сюрприз кроется в деталях. Дело в том, что более трехсот лет назад Ньютон провозгласил, что свет представляет собой поток частиц, так что сама идея не нова. Однако ряд коллег Ньютона, среди которых наиболее выделялся голландский физик Христиан Гюйгенс, оспорили это мнение, утверждая, что свет представляет собой волну. Долгое время этот вопрос был предметом ожесточенных дебатов, пока эксперименты, выполненные в начале XIX в. английским физиком Томасом Юнгом, не показали, что Ньютон ошибался.

Вариант установки в эксперименте Юнга, известном под названием опыта с двумя щелями, схематически показан на рис. 4.3. Фейнман любил говорить, что вся квантовая механика может быть выведена путем тщательного осмысливания следствий одного этого эксперимента, поэтому он заслуживает того, чтобы рассмотреть его поподробнее. Как видно из рис. 4.3, свет падает на сплошную преграду, в которой сделаны две щели. Свет, который прошел через щели, регистрируется на фотопластинке — более светлые области на фотографии указывают на те места, куда попало больше света. Эксперимент состоит в сравнении картин, полученных на фотопластинках, когда открыты одна или обе щели и включен источник света.

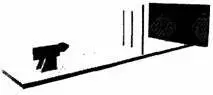
Рис. 4.3. В эксперименте с двумя щелями луч света падает на преграду, в которой проделаны две щели. Когда открыта одна или обе щели, луч света, проходящий через преграду, регистрируется с помощью фотопластинки.

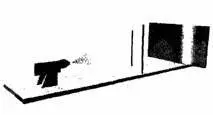
Рис. 4.4. В этом опыте открыта правая щель, в результате изображение на фотопластинке будет выглядеть, как показано на рисунке.

Если левая щель закрыта, а правая открыта, фотография будет выглядеть, как показано на рис. 4.4. Картина вполне объяснима, поскольку свет, который попадает на фотопластинку, проходит только через одну щель и поэтому концентрируется в правой части фотографии. Аналогично, если мы закроем правую щель, а левую оставим открытой, фотография будет выглядеть, как показано на рис. 4.5.

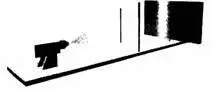
Рис. 4.5. Те же условия, как и в опыте, показанном на рис. 4.4, за исключением того, что открыта левая щель.

Если открыты обе щели, то картина, предсказываемая ньютоновской корпускулярной моделью света, должна выглядеть, как показано на рис. 4.6, представляющем собой комбинацию рис. 4.4 и 4.5.

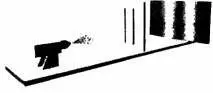
Рис. 4.6. Ньютоновская корпускулярная модель предсказывает, что когда будут открыты обе щели, картина на фотопластинке будет представлять собой объединение картин, показанных на рис. 4.4 и 4.5.

По существу, если представить ньютоновские световые корпускулы в виде маленьких дробинок, которыми вы обстреливаете преграду, то те из дробинок, которые пройдут сквозь нее, будут концентрироваться в двух полосах, положение которых соответствует положению щелей. Волновая же модель света, напротив, ведет к совершенно иному предсказанию, если открыты обе щели. Посмотрим, что происходит в этом случае.

Представим, что вместо световых волн мы рассматриваем волны на поверхности воды. Это не повлияет на результат, но такие волны более наглядны. Когда волна сталкивается с преградой, то, как показано на рис. 4.7, от каждой щели распространяется новая волна, похожая на ту, которая возникает, если бросить камешек в пруд. (Это легко проверить, используя картонный лист с двумя прорезями, помещенный в чашку с водой.) Когда волны, идущие от каждой щели, накладываются друг на друга, происходит интересное явление. При наложении двух волновых максимумов высота волны в соответствующей точке увеличивается — она равна сумме высот максимумов двух наложившихся волн. Аналогично, при наложении двух минимумов глубина впадины, образовавшейся в этой точке, также увеличивается. Наконец, если максимум одной волны совпадает с минимумом другой, они взаимно гасят друг друга. (На этом основана конструкция фантастических шумопоглощающих наушников — они определяют форму пришедшей звуковой волны и генерируют другую, форма которой в точности «противоположна» первой, что приводит к подавлению нежелательного шума.) Между этими крайними случаями — максимум с максимумом, минимум с минимумом и максимум с минимумом — расположен весь спектр частичного усиления и частичного ослабления. Если вы с компанией друзей сядете в небольшие лодки, выстроите их в линию параллельно преграде и каждый из вас будет сообщать, насколько сильно его качает при прохождении волны, результат будет похож на тот, который изображен на рис. 4.7.