Девид Дойч - Структура реальности

Существуют физические объекты, например, пальцы, компьютеры и мозг, поведение которых может моделировать поведение определенных абстрактных объектов. Таким образом, структура физической реальности дает нам окно в мир абстракций. Это очень узкое окно, оно предоставляет только ограниченный диапазон перспектив. Некоторые из структур, которые мы видим из него, например, натуральные числа или правила вывода классической логики, кажутся такими же важными или «фундаментальными» для абстрактного мира, какими глубокие законы природы являются для физического мира. Но эта видимость может ввести в заблуждение. Поскольку действительно мы видим только то, что некоторые абстрактные структуры фундаментальны по отно шению к нашему пониманию абстракций, у нас нет никакой причины считать, что эти структуры объективно важны в абстрактном мире. Просто некоторые абстрактные категории ближе, чем другие, и их проще увидеть из нашего окна.

Математика – изучение абсолютно необходимых истин.

Доказательство – способ установления истинности математических высказываний.

(Традиционное определение): последовательность утверждений, которая начинается с некоторых посылок, заканчивается желаемым выводом и удовлетворяет определенным «правилам вывода».

(Лучшее определение): вычисление, моделирующее свойства какой-то абстрактной категории, результат которого устанавливает, что абстрактная категория обладает данным свойством.

Математическая интуиция (традиционное) – высший самоочевидный источник доказательства в математическом рассуждении.

(Действительное): Множество теорий (осознанных и неосознанных) о поведении определенных физических объектов, поведение которых моделирует поведение интересных абстрактных категорий.

Интуиционизм – доктрина, связанная с тем, что все рассуждение об абстрактных категориях ненадежно, кроме того случая, когда оно основано на прямой самоочевидной интуиции. Это математическая версия солипсизма.

Десятая задача Гильберта – «раз и навсегда установить определенность математических методов», найдя набор правил вывода, достаточный для всех обоснованных доказательств, и затем доказать состоятельность этих правил в соответствии с их собственными нормами.

Теорема Геделя о неполноте – доказательство того, что десятая задача Гильберта не имеет решения. Для любого набора правил вывода существуют обоснованные доказательства, которые эти правила не определяют как таковые.

Сложные и автономные абстрактные категории объективно существуют и являются частью структуры реальности. Существуют логически необходимые истины об этих категориях, которые и составляют предмет математики. Однако, эти истины невозможно знать определенно. Доказательства не дают их выводам определенность. Обоснованность конкретной формы доказательства зависит от истинности наших теорий о поведении объектов, с помощью которых мы осуществляем доказательство. Следовательно, математическое знание наследственно производно и полностью зависит от нашего знания физики. Постижимые математические истины – это в точности то бесконечно малое меньшинство, которое можно передать в виртуальной реальности. Однако непостижимые математические категории (например, среды Кантгоуту) тоже существуют, т. к. они сложным образом появляются в наших объяснениях постижимых категорий.

Я сказал, что вычисление всегда было квантовой концепцией, потому что классическая физика несовместима с интуицией, создавшей основу классической теории вычисления. То же самое относится ко времени. За тысячу лет до квантовой теории время было первой квантовой концепцией.

Даже будучи одним из наиболее знакомых свойств физического мира, время имеет репутацию глубоко загадочного. Загадка – часть самого понятия времени, с которым мы растем. Святой Августин, например, сказал:

«Что же тогда есть время? Если никто не спросит меня, я знаю; если я захочу объяснить это тому, кто спросит, я не знаю». ( Confessions [17] )

Мало кто считает, что расстояние загадочно, но то, что время загадочно, знают все. И вся загадочность времени проистекает из его основного логического свойства, а именно, что настоящий момент, который мы называем «сейчас», не стационарен, а постоянно движется в направлении будущего. Это движение называется потоком времени.

Мы увидим, что потока времени не существует. Тем не менее, такое представление совершенно обыденно. Мы принимаем это как должное настолько, что это принимается в самой структуре нашего языка. В книге A Comprehensive Grammar of the English Language [18]Рэндольф Квирк и его соавторы объясняют концепцию времени с помощью диаграммы, показанной на рисунке 11.1. Каждая точка на линии представляет конкретный стационарный момент. Треугольник «s» показывает, где на линии расположена «непрерывно движущаяся точка, настоящий момент». Считается, что она движется слева направо. Некоторые люди, как Шекспир в процитированном выше сонете, считают определенные события «стационарными», а саму линию движущейся мимо них (справа налево на рисунке 11.1), так что моменты из будущего проносятся мимо настоящего момента, чтобы стать прошлыми моментами.

«время можно считать линией (теоретически, линией бесконечной длинны), на которой расположен, как постоянно движущаяся точка, настоящий момент.

Все что находится перед настоящим моментом, – в будущем, все что находится за настоящим моментом, – в прошлом».

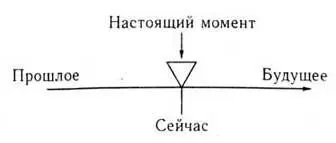
Рис. 11.1. Общеизвестная концепция времени, принятая в английском языке (основанная на Квирк и др. A Comprehensive Grammar of the English Language, с. 175)

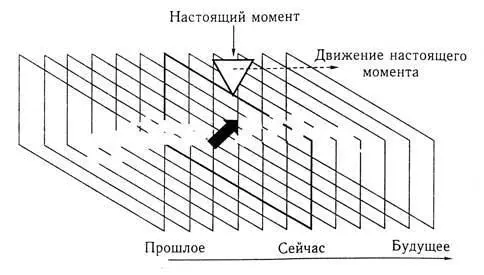
Рис. 11.2. Движущийся объект как последовательность «снимков», которые один за другим становятся настоящим моментом

Что мы подразумеваем под высказыванием «время можно считать линией»? Мы подразумеваем, что точно так же, как линию можно считать последовательностью точек в различных положениях, так и любой движущийся или изменяющийся объект можно считать последовательностью неподвижных вариантов «снимков» самого себя, по одному варианту в каждый момент. Сказать, что каждая точка линии представляет конкретный момент, все равно, что сказать, что можно представить все снимки собранными вдоль линии, как на рисунке 11.2. Некоторые из них показывают вращающуюся стрелку, какой она была в прошлом, Другие показывают, какой она будет в будущем, а один из них – тот, на который сейчас показывает движущийся s – показывает стрелку такой, какая она сейчас, хотя через мгновение этот конкретный вариант стрелки будет в прошлом, потому что s передвинется. Совокупность мгновенных вариантов объекта является движущимся объектом в том же смысле, в каком последовательность неподвижных картинок, спроецированных на экран, в совокупности является фильмом (движущейся картинкой). Ни одна из них в отдельности не изменяется. Изменение состоит в том, что в последовательности на них указывает («освещает») движущийся s («кинопроектор»), так что друг за другом, по очереди они оказываются в настоящем моменте.