Виктор Петров - Искусственный спутник земли

Эта задача является весьма сложной, и ее решение будет одним из основных факторов, отличающих автоматизированный ИСЗ от неавтоматизированного. Она осуществляется путем системы астроориентировки и стабилизации.

Как только спутник отделится от ракеты-носителя и начнет совершать по орбите самостоятельный полет, эта система должна вступить в действие. Для того чтобы понять физический принцип этой системы, необходимо вспомнить некоторые астрономические и географические понятия.

Как известно, положение любой точки на земной поверхности может быть определено двумя ее координатами — долготой λ и широтой φ.

Через ось вращения Земли можно провести сколько угодно плоскостей, пересечение которых с земной поверхностью образует воображаемые линии, называемые меридианами. Перпендикулярно к этим плоскостям также можно расположить сколько угодно плоскостей, пересечение которых с земной поверхностью образует воображаемые линии, называемые параллелями. Одна из таких параллелей, проходящая через центр Земли, называется экватором.

Угол между линией, проходящей через центр Земли и через любую точку, находящуюся на поверхности Земли, скажем, точку А (указанную на рис. 46), и плоскостью экватора называется широтой места данной точки (на нашем рисунке угол АОВ ). Его можно заменить также дугой АВ и измерять в градусах, минутах или секундах дуги.

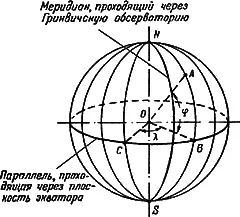
Все значения широты, лежащие в северном полушарий, принято считать положительными, а в южном — отрицательными. Долготу места принято измерять к востоку или к западу от меридиана, проходящего через Гринвичскую обсерваторию (находящуюся в Англии). Долготой называется величина дуги экватора между Гринвичским меридианом и меридианом, проведенным через данную точку. В нашем случае долготой будет дуга СВ .

Восточную долготу принято считать положительной, западную — отрицательной.

Из рис. 46 видно, что, зная географическую долготу и широту места, мы можем точно определить положение объекта на земной поверхности.

Обратимся теперь к рис. 47.

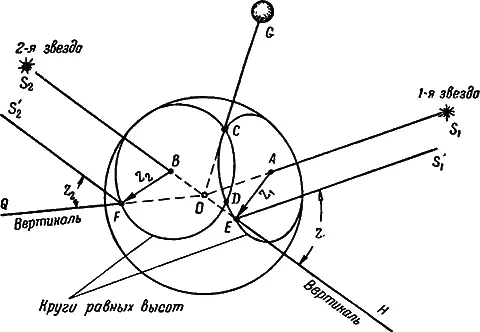
Здесь изображен земной шар, два светила (звезды) и искусственный спутник Земли G .

Представим себе, что мы из центра Земли провели прямую линию, соединяющую ее со звездой, скажем, с первой, обозначенной на рис. 47 буквой S 1. Эта линия пересечет земную поверхность в точке А . Человек, который находится в этой точке, будет видеть первую звезду в зените, т. е. прямо над головой. Если он удалится от этой точки в любую сторону, то будет видеть эту звезду уже не прямо над головой, а под некоторым углом, причем этот угол будет изменяться вследствие шарообразности Земли в зависимости от удаления его от этой точки. Точка А или В называется географическим местом светила и обозначается сокращенно ГМС.

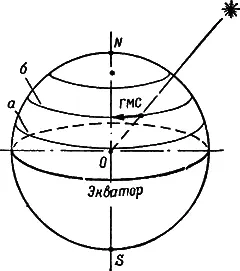
ГМС перемещается по земной поверхности со скоростью один оборот вокруг оси Земли в звездные сутки [32], причем его путь будет совпадать с какой-либо из параллелей (рис. 48) а и б . Из этого следует, что широта ГМС в каждом отдельном случае будет известной и постоянной, а изменение долготы, т. е. скорость перемещения ГМС по параллели, происходит строго закономерно (15 дуговых градусов за час звездного времени).

Пусть человек удалился от ГМС (точка А ) в точку Е . Из рис. 47 ясно видно, что, двигаясь по окружности вокруг точки А , человек будет всегда видеть первую звезду под одним и тем же углом относительно плоскости горизонта, называемым высотой светила. Эта окружность на земной поверхности называется кругом равных высот.

Угол между направлением на светило, взятым из какой-либо точки (например, точки E ), лежащей на круге равных высот, и вертикалью (на нашем рисунке угол АOЕ = Z 1и FOB = Z 2, так как лучи, идущие от звезд S 1и S 2, вследствие их огромной удаленности являются параллельными) называется зенитным расстоянием. Сумма углов зенитного расстояния и высоты светила равна 90°.

Лучи, идущие от первой звезды S 1 A и S 2 1 F , равно, как и лучи S 2 B и S 2 1 F , идущие от второй звезды, соответственно параллельны.

Теперь обратимся к искусственному спутнику Земли. Для него, так же как и для звезд, мы будем иметь вертикаль OG (линия, соединяющая центр Земли с ИСЗ) и его географическое место, лежащее в точке пересечения этой вертикали с земной поверхностью, т. е. в точке С .

Очевидно, положение ИСЗ можно определить тремя координатами — широтой и долготой географического места ИСЗ и высотой относительно поверхности Земли.

В связи с этим астронавигация искусственного спутника Земли разбивается на два этапа: во-первых, определяется широта и долгота географического места ИСЗ каким-либо астрономическим способом, причем его существо не отличается от принятых в мореходной и авиационной навигации способов, во-вторых, определяется высота искусственного спутника Земли над Землей. Выполнение обоих этапов астронавигационных измерений и дает полное представление о положении искусственного спутника Земли в пространстве.

Определение координат ИСЗ может быть осуществлено наземными оптическими, радиолокационными и радионавигационными средствами, а также с помощью астрономических приборов, располагаемых на ИСЗ.

С точки зрения научного и военного использования ИСЗ имеют наибольший интерес автономные астрономические методы определения координат ИСЗ, осуществляемые непосредственно со спутника. Автономные методы ориентировки не подвержены каким-либо искусственным помехам и отличаются высокой точностью измерений.