Лоуренс Краусс - Страх физики. Сферический конь в вакууме

Если наш пещерный житель воспользуется тенью от линейки для измерения расстояния, он обнаружит, что размеры одних и тех же предметов, измеряемые им, постоянно оказываются разными. Мы, не ограниченные двумерной стеной пещеры и живущие в трехмерном мире, могли бы найти решение проблемы, обратив внимание на то, что длина тени на стене зависит от угла, под которым расположена линейка по отношению к стене и к источнику света.

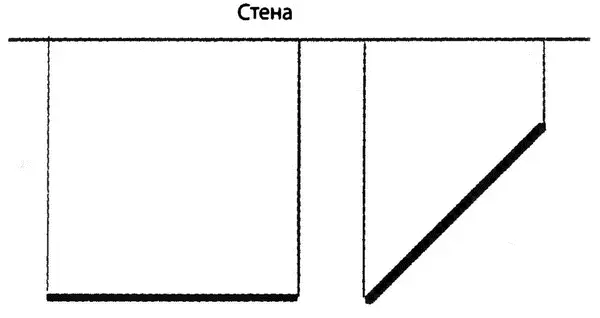
Затем мы бы заметили, что, когда линейка поворачивается, ее длина не изменяется, но изменяется длина проекции линейки на стену. Например, когда две стены образуют прямой угол, проекции линейки на эти стены будут выглядеть следующим образом:

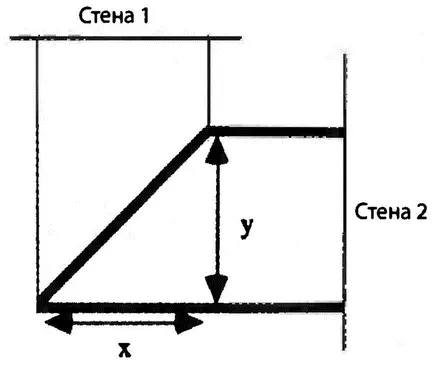
Если длина линейки — L, то, согласно теореме Пифагора, L 2= x 2+ y 2. Таким образом, даже когда отдельные проекции x и y изменяются, сумма их квадратов всегда остается постоянной. В тот момент, когда для исследователя, наблюдающего только y-проекцию, «измеряемая» им длина линейки становится равной нулю, для исследователя, наблюдающего только x-проекцию, «измеряемая» длина линейки максимальна, и наоборот.

Математически именно так ведут себя пространство и время для двух наблюдателей, движущихся относительно друг друга. Движущийся поезд сокращается относительно неподвижного наблюдателя в пространстве, то есть становится короче, однако «растягивается» во времени в том смысле, что часы в движущемся поезде идут медленнее, чем часы неподвижного наблюдателя.

Еще важнее то, что упомянутая величина s является в теории относительности аналогом длины линейки L из предыдущего примера. Эта мера — s — называется пространственно-временным интервалом и определяется как s 2= с 2t 2— d 2. Она представляет собой комбинацию пространственного и временного интервалов между событиями и всегда равна нулю для двух событий, лежащих на пространственно-временной траектории луча света. То есть если свет, испущенный из точки, в которой происходит первое событие, достигает точки, в которой происходит второе событие в момент этого события, то пространственно-временной интервал между этими событиями равен нулю. Интервал одинаков для всех наблюдателей, независимо от того, как они движутся друг относительно друга. Если два события не лежат на пространственно-временной траектории луча света, то интервал между ними будет отличен от нуля, но он по-прежнему будет одним и тем же для всех наблюдателей.

Таким образом, интервал s является, как говорят, инвариантом в теории относительности. Интервал для движущихся по-разному наблюдателей представляет собой то же, что длина линейки для пещерных обитателей. В теории относительности интервал — это пространственно-временная длина. Три пространственных измерения и время оказываются тесно связанными друг с другом, наподобие того, как тесно связаны две проекции линейки на стенах пещеры. Движение объекта приводит к изменению проекции четырехмерного пространства-времени на трехмерную сцену, которую мы называем словом «сейчас», подобно тому как поворот линейки приводит к изменению ее двухмерной проекции на стену пещеры! Эйнштейн, руководствуясь постулатом о постоянстве скорости света, получил возможность сделать то, о чем большинство из нас могло бы только мечтать. Он выглянул за стены пещеры и увидел доселе скрытую от него реальность, подобно тому как наш персонаж однажды обнаружил, что круглая и прямоугольная тени на стене пещеры принадлежат цилиндрическому контейнеру. Но к чести Эйнштейна, он на этом не остановился. Картина еще не была завершена. Его путеводной нитью снова оказался луч света. В се наблюдатели, движущиеся с постоянной скоростью, видят луч света, движущийся относительно них со скоростью с, и ни один из них не может утверждать, что он покоится, в то время как движутся все остальные. Движение относительно. Но что, если скорость движения наблюдателей не постоянна! Что, если один из них движется с ускорением? Смогут ли в этом случае все наблюдатели, включая ускоряющегося, однозначно утверждать, что один из них движется с ускорением? Чтобы исследовать этот вопрос, Эйнштейн придумал еще один мысленный эксперимент. Как вы определяете, находясь в лифте, когда и в каком направлении он начинает движение? Когда лифт начинает движение вверх, вы чувствуете, что стали немного тяжелее; когда же лифт начинает двигаться вниз, вы ощущаете, что стали легче. Но откуда вы знаете, что изменение вашего веса вызвано ускорением лифта, а не изменением силы тяжести?

Не спешите с ответом. Не существует ни одного эксперимента, который дал бы запертому в лифте наблюдателю ответ, движется лифт с ускорением или покоится в гравитационном поле. Давайте упростим мысленный эксперимент. Пусть лифт находится в глубоком космосе вдали от тяготеющих тел. Когда он находится в состоянии покоя или движется равномерно и прямолинейно, мы испытываем внутри него полную невесомость. Если лифт начнет ускоряться, скажем, вверх, его пол начнет давить на ноги, чтобы придать вам такое же ускорение, которое испытывает он сам. Если вы выпустите мяч из ваших рук, он начнет «падать» на пол. Почему? Потому что если мяч первоначально находился в состоянии покоя, то он, согласно Галилею, будет стремиться сохранить это состояние, однако пол-лифта движется вверх с ускорением и в конце концов настигнет мяч. С вашей точки зрения, это будет выглядеть, как будто мяч с ускорением полетел вниз и ударился об пол. Более того, ускорение мяча не зависит от его массы. Действительно, какой бы мяч вы ни взяли, пол лифта настигнет его через тот же самый промежуток времени.

Если бы Галилей оказался вместе с вами в лифте, он мог бы поклясться, что находится на Земле. Все опыты с падающими телами, которые он поставил за свою жизнь, будут проходить в таком лифте точно так же, как и на поверхности Земли. Таким образом, если Галилей пришел к выводу, что все законы физики выполняются одинаково во всех системах отсчета, движущихся равномерно и прямолинейно, то Эйнштейн пошел дальше и понял, что законы физики должны быть одинаковы для системы отсчета, движущейся с постоянным ускорением, и для системы отсчета, покоящейся в гравитационном поле. С этой точки зрения ускорение тоже относительно, просто один наблюдатель назовет его ускорением, а другой — гравитацией.

Снова Эйнштейн выглянул за пределы пещеры. Если гравитация может быть «создана» внутри лифта, то, может быть, мы все живем внутри метафорического лифта? Может быть, то, что мы называем гравитацией, на самом деле является ускорением, и все зависит только от выбранной точки зрения? Мы живем на Земле. Земля обладает большой массой. Возможно, то, что мы воспринимаем как силу притяжения между двумя массами, является результатом какого-нибудь хитрого искажения окружающего нас пространства-времени?