Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

Роберт Бойль(1626–1691). Великий экспериментатор, изучавший физику вакуума, законы поведения идеальных газов, химию. Один из первых членов Королевского общества. Написал трактат «Химик-скептик».

Христиан Гюйгенс(1629–1695). Математик и физик, создатель волновой теории света. Сконструировал очень точные часы (вероятно, первую модель маятниковых часов) с корректирующим устройством, учитывающим незначительное увеличение периода маятника при большой амплитуде. Занимался исследованиями в области механики и еще до Ньютона вывел выражение v 2/ R для центростремительного ускорения.

Роберт Гук(1632–1702). Начал заниматься научной работой как ассистент Бойля, но вскоре достиг значительных успехов, и получил большую известность как экспериментатор и как теоретик. Его соперничество с Ньютоном приносило ему много огорчений; гениальные труды Ньютона затмевали его собственные и умаляли его достижения. Если бы не это соперничество, в котором победителем оставался гений Ньютона, Гука можно было бы считать одним из величайших ученых XVII века. Гук с горечью утверждал, что некоторые достижения Ньютона в области механики фактически открыты им, Гуком, еще раньше. Гук был одним из первых членов Лондонского Королевского общества.

Эдмунд Галлей(1656–1742). Астроном, друг Ньютона. Много сделал для того, чтобы помочь публикации «Принципов» Ньютона. Один из наиболее значительных членов Королевского общества.

Наука

В тот период наука развивалась по пяти основным направлениям: 1) по мере роста свободы слова росло и общее значение науки, основанной на эксперименте; 2) происходило накопление фактических знаний и теории , объясняющей полученные результаты; 3) развивались математические методы для решения тех или иных задач; 4) изобретались и конструировались новые приборы для проведения экспериментов и, наконец, 5) изменялись научные методы и отношение к науке .

1) Возросшее значение науки . На примере жизни Галилея мы уже видели, как возросло значение науки в ту эпоху. Отец Галилея считал математику да и науку вообще плохо оплачиваемым и малоуважаемым занятием, и все же Галилей, несмотря на бунтарский нрав, в конце жизни был уважаем как один из величайших людей в мире. Ньютону, Бойлю и Гуку не приходилось отстаивать свои научные позиции; они спорили лишь о своих открытиях, а не о праве на само открытие. Они писали свои труды, не страшась осуждения и не боясь показаться смешными, их заботили лишь приоритет и слава. Дискуссии и публикации трудов помогали науке становиться общенародной и универсальной. Так истинность науки начала воздействовать на человеческий разум.

2) Накопление знаний . Научные достижения XVII века значительны и многообразны: к ним следует отнести законы Кеплера, открытие кометы Галлея, закон Гука, открытие Гарвеем системы кровообращения, открытия Бойля в области химии и его закон для идеальных газов.

3) Достижения в области математики. Была изобретена декартова система координат. Графики связали алгебру с геометрией, с одной стороны, сводя геометрические формы и преобразования к сжатым алгебраическим выражениям, а с другой — позволяя наглядно представлять алгебраические уравнения.

На графике I фиг. 98 изображена проходящая через начало координат прямая линия, на которой нанесены точки ( x 1, y 1), ( x 2, y 2)…. Из подобия треугольников следует, что отношения y 1/ x 1, y 2/ x 2…. равны между собой, т. е. одинаковы для любой точки на прямой. Обозначим эту постоянную k . Тогда каждая точка на прямой будет представлена парой значений (например, x 1, y 1), удовлетворяющих соотношению у / х = k или у = kх . Это и есть алгебраическое описание графика, а прямая представляет собой геометрический образ данного соотношения. Если у и х — результаты физических измерений (например, s и t 2для падающего тела), то прямая линия выражает соотношение y = (const) x , или у ~ х , а наклон прямой определяет постоянную.

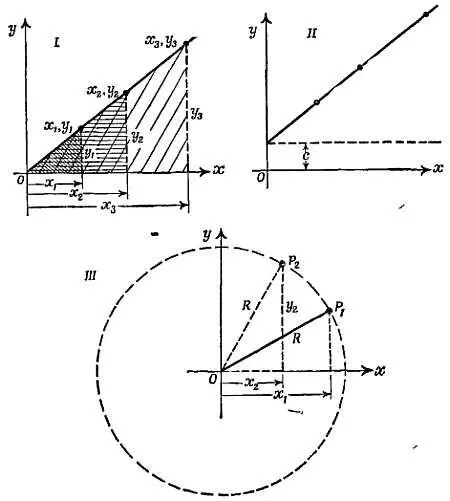
Фиг. 98. Графики в декартовой системе координат.

График II иллюстрирует уравнение у= k х+ с. В этом случае мы не можем сказать, что у ~ х , но можем сказать, что Δ у ~ Δх .

На графике III изображена окружность, причем

для точки P 1

x 2 1+ у 2 1= R 2

для точки P 2

x 2 2+ у 2 2= R 2

таким образом, уравнение этой окружности имеет вид

x 2+ у 2= R 2

Его можно переписать так:

x 2/ R 2+ y 2/ R 2= 1

Эллипс можно получить равномерным растяжением окружности.

Нарисуйте окружность на листе резины и растяните этот лист (фиг. 99).

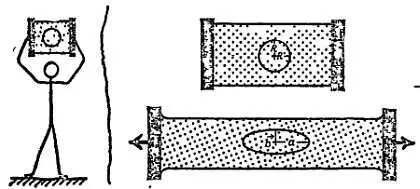
Фиг. 99. Растяжение окружности в эллипс.

Радиус R превратится в полуоси а и b . Окружность в соответствии о уравнением x 2/ R 2+ y 2/ R 2= 1 и с площадью круга π R 2= π∙ R∙ Rпревратится в эллипс, описываемый уравнением…?.. = 1 и площадью =?

Таким образом, с помощью декартовой геометрии эллиптические орбиты можно записать в виде алгебраических уравнений.

Возникли две серьезные математические проблемы, связанные с вычислениями: определение угла наклона касательных к кривым и площадей под кривыми с помощью математики , т. е. создание методов дифференцирования и интегрирования . Тангенс угла наклона касательной определяет скорость изменения функции. Вычисления сводятся просто к нахождению скорости изменения функции в некоторой точке. Это позволяет нам вычислять ускорения из выражения, описывающего изменение скорости , или скорости из выражения, связывающего расстояние и время . (Например: если s= 16 t 2, то v= 32 t; отсюда следует, что а= 32, т. е. постоянное значение.) Интегрирование — операция сложения бесконечно большого числа бесконечно малых величин: нахождение площади путем сложения элементов исчезающе малых размеров (как и в случае второго закона Кеплера) или нахождение силы притяжения между телами конечных размеров путем суммирования сил притяжения бесконечно малых элементов объема этих тел.

Вы уже пользовались графиками и вычислениями ранее, при решении задачи о колесе, катящемся вниз с холма.