Эрик Роджерс - Физика для любознательных. Том 2. Наука о Земле и Вселенной. Молекулы и энергия

б) Радиус атома водорода ( n ~= 1) примерно равен 0,5 А° (0,5∙10 -10м). Возбужденные атомы водорода наблюдаются в звездах с n , равным 30. Каков «размер» такого атома?

Идеи закона всемирного тяготения уже «витали в воздухе», когда Ньютон производил свои расчеты. Ряд ученых размышлял о том, что лежит в основе законов Кеплера. Делались попытки ответить на вопрос, можно ли объяснить движение планет притяжением Солнца, которое ослабевает по мере удаления от него. Ньютон извлек доказательство из моря домыслов и расширил предположение о силе притяжения Солнцем до понятия о всемирном тяготении. Он проверил свое предположение об обратной пропорциональности силы квадрату расстояния, рассмотрев движение Луны, и на основе этого пришел к законам Кеплера. Последующие проверки этой идеи на движении спутников Юпитера показали, что между планетами и их спутниками действуют силы того же типа, что и между Солнцем и планетами. Таким образом, на основе экспериментальных доказательств множитель 1/ d 2в соотношении F= GM 1 M 2/ d 2был вполне обоснован для случая Солнечной системы.

Символический эксперимент Галилея (фиг. 182) определяет множитель М 2, т. е. массу притягиваемого тела. Так как ускорение свободного падения g одинаково для всех тел, Земля должна притягивать их с силой, пропорциональной их массам М 2, М' 2.

Фиг 182. Символический эксперимент Галилея.

Ньютон полагался на свой третий закон (действие равно противодействию), который он считал частично подтвержденным в опытах с маятником по проверке сохранения количества движения. Гравитационное воздействие М 1на М 2должно быть равно и противоположно гравитационному воздействию М 2на М 1, т. е. 1 F 2= 2 F 1. Поэтому G должно быть одинаковым для обеих сил:

1 F 2= G( M 1 M 2)/ d 2,

2 F 1= G( M 2 M 1)/ d 2

Таким образом, притягиваемое и притягивающее тела взаимозаменимы и гравитационное притяжение должно быть пропорционально массе притягиваемого тела. Это кажется очень правдоподобным, даже несомненным для всех, кто верит в симметрию; однако проверить это экспериментально на основе астрономических измерений нельзя, поскольку мы сможем определить массы астрономических тел только тогда, когда космонавты доставят нам образцы и представят результаты своих наблюдений. На основе своей теории Ньютону удалось оценить отношения масс небесных тел; ( масса Юпитера )/( масса Солнца ), ( масса Земли )/( масса Солнца ) и даже, основываясь на догадках о роли приливов, отношение ( масса Луны )/( масса Солнца ), но он не мог вычислить массу каждого из этих тел в отдельности, так как не знал величины гравитационной постоянной G . Для определения величины G надо было выполнить в лаборатории эксперименты по измерению очень слабого притяжения между двумя телами с известными массами.

Измерение величины G

Величина гравитационной постоянной G оставалась неизвестной еще спустя полвека после Ньютона. Оценки величины G на основе предположений, подобных гипотезе Ньютона о средней плотности Земли, показали, что гравитационное притяжение тел в лабораторной обстановке должно быть безнадежно малым. Обычно сила тяжести кажется большой, так как обусловлена громадной массой Земли. А Солнце, обладая чрезвычайно большой массой, управляет всей планетной системой. Гравитационное притяжение тел привычных нам размеров настолько мало, что мы не замечаем его по сравнению с притяжением Земли и силами с малым радиусом действия, возникающими между телами, когда те находятся в «контакте». Поэтому стало ясно, что измерение G потребует тонких и сложных экспериментов.

В конце XVIII столетия несколько ученых предприняли отчаянную попытку провести такой эксперимент, используя в качестве притягивающего тела гору известных размеров. Они оценили значение G , измеряя притяжение горой расположенного вблизи нее маятника. Чисто астрономическим путем было измерено крошечное отклонение маятника от вертикали, обусловленное притяжением горы. С помощью геологии они оценили массу горы и ее «среднее расстояние» от маятника. Подставляя результаты этих измерений в формулу F= GM 1 M 2/ d 2, они получили величину G .

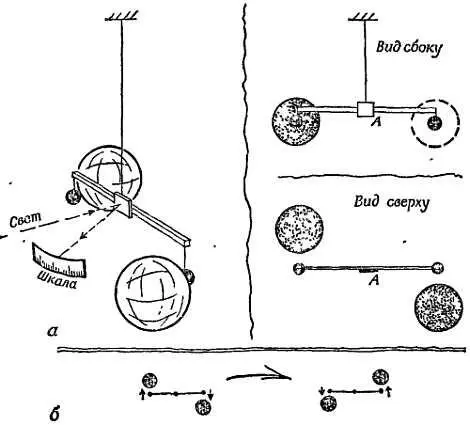
Фиг. 183 Установка Кавендиша.

а— планка, несущая маленькие свинцовые шарики, закручивание нити становится зaметным благодаря лучу света, отражающемуся от маленького зеркала А ; б— для удвоения угла поворота большие шары помещались так, чтобы планка разворачивалась в противоположных направлениях.

Примерно в то же время Кавендиш, а позже и многие другие измерили методом прямого «взвешивания» гравитационное притяжение между массивными кусками металла и маленьким металлическим шариком. Кавендиш прикрепил пару маленьких металлических шариков к легкой планке, подвешенной в виде трапеции на длинной тонкой нити. К маленьким шарикам он подносил большие свинцовые шары. В результате воздействия этих шаров на маленькие планка поворачивалась и закручивала нить до тех пор, пока эффект притяжения не компенсировался силами Гука в закрученной нити. Кавендиш измерил массы и расстояние от маленьких шариков до больших; для вычисления величины G ему надо было знать силу притяжения, т. е. упругую силу закручивания нити.

Для прямых измерений нить была слишком тонкой и непрочной. Поэтому Кавендиш измерял период простых гармонических колебаний планки (см. гл. 10 [107]). Измерив также массу и размеры планки, он смог вычислить силу закручивания нити. Так он получил хорошую оценку величины G , которую подтвердили в аналогичных более тщательных экспериментах Бойс, Гейл и др. Во всех случаях использовалась столь чувствительная аппаратура, что даже слабые воздушные потоки могли исказить измерения. Чтобы избежать конвекции, Кавендиш разместил свою аппаратуру в ящике, затем поставил ящик в закрытой комнате и проводил наблюдения за аппаратурой с помощью телескопа из другого помещения.

Результаты измерения G

В приведенной на стр. 300 таблице собраны некоторые данные, полученные в многочисленных экспериментах по измерению величины G , выполненных за минувшие 220 лет. Она не только демонстрирует все возрастающую достоверность измеренных значений этой важной величины, но и служит хорошей основой для проверки соотношений