Митио Каку - Гиперпространство: Научная одиссея через параллельные миры, дыры во времени и десятое измерение

Но и Солнце не сможет существовать в мире высших измерений. Сила гравитации стремится сжать Солнце, ее уравновешивает сила термоядерных реакций, которая стремится разорвать его. Таким образом, Солнце – результат точного равновесия сил ядерного взаимодействия, способных взорвать его, и сил гравитационного взаимодействия, способных сжать его в точку. В многомерной Вселенной это шаткое равновесие неизбежно нарушится, что приведет к спонтанному схлопыванию звезд.

Хендерсон «Четыре измерения и неевклидова геометрия в современном искусстве», с. 22.

Цёлльнер обратился в спиритуализм в 1875 г., когда побывал в лаборатории Крукса – первооткрывателя элемента таллия, изобретателя катодно-лучевой трубки, редактора научного журнала Quarterly Journal of Science . Катодно-лучевая трубка Крукса произвела революцию в науке: каждый, кто смотрит телевизор, пользуется компьютерным монитором, играет в видеоигры или проходит рентгеновское обследование, обязан всему этому знаменитому изобретению Крукса.

Крукс не был сумасбродом. Он занимал видное положение в британском научном сообществе, его профессиональных наград хватило бы на украшение целой стены. В 1897 г. его посвятили в рыцари, в 1910 г. удостоили ордена «За заслуги». Живой интерес к спиритуализму пробудила в нем трагическая смерть брата Филипа, в 1867 г. умершего от желтой лихорадки. Крукс стал видным членом, а позднее и президентом Общества паранормальных (психических) исследований, в которое входили многие выдающиеся ученые конца XIX в.

Процитировано в: Руди Рукер «Четвертое измерение» (Rudy Rucker, The Fourth Dimension, Boston: Houghton Mifflin, 1984), с. 54.

Для того чтобы представить себе, как можно распутать узлы в измерениях, числом превышающих три, вообразим себе два сцепленных кольца. Теперь сделаем двумерный поперечный разрез этой конструкции таким образом, чтобы одно кольцо лежало в плоскости разреза, а второе превратилось в точку (поскольку оно лежит перпендикулярно этой плоскости). Мы получили точку внутри окружности. В высших измерениях мы имеем возможность вывести эту точку за пределы окружности, не разрезая ни одно из колец. Это означает, что два кольца теперь разделены, что нам и требовалось. Значит, узлы в условиях многомерности всегда можно развязать, потому что для этого «достаточно места». Обратите также внимание: вывести точку за пределы окружности в трехмерном пространстве невозможно, по той же причине в мире трех измерений узлы остаются завязанными.

Герберт Уэллс «Машина времени» (H. G. Wells, The Time Machine: An Invention, London: Heinemann, 1895), с. 3.

Линда Далримпл Хендерсон «Четвертое измерение и неевклидова геометрия в современном искусстве» (Linda Dalrymple Henderson, The Fourth Dimension and Non-Euclidean Geometry in Modern Art, Princeton, N. J.: Princeton University Press, 1983), с. xxi.

Там же. Согласно Хендерсон, «четвертое измерение привлекало внимание таких видных представителей мира литературы, как Герберт Уэллс, Оскар Уайльд, Джозеф Конрад, Форд Мэдокс Форд, Марсель Пруст и Гертруда Стайн. Из музыкантов четвертым измерением живо интересовались Александр Скрябин, Эдгар Варез, Джордж Антейл, оно вдохновляло их поиски новых форм во имя высшей реальности» (там же, с. xix – xx).

Работа Ленина «Материализм и эмпириокритицизм» сегодня имеет большое значение по той причине, что она оставила заметный след в современной советской и восточноевропейской науке. К примеру, известное высказывание Ленина о «неисчерпаемости электрона» отражало диалектическую идею, согласно которой мы найдем новые уровни и противоречия при любой попытке проникнуть в суть материи. Так, галактики состоят из меньших по размеру звездных систем, которые в свою очередь содержат планеты, состоящие из молекул, которые состоят из атомов, содержащих электроны, а те, в свою очередь, «неисчерпаемы». Это один из вариантов теории «миров, заключенных в других мирах».

Владимир Ленин. Материализм и эмпириокритицизм // Карл Маркс, Фридрих Энгельс и Владимир Ленин. О диалектическом материализме. – М.: Прогресс, 1977. – С. 305–306.

Владимир Ленин. Материализм и эмпириокритицизм // Карл Маркс, Фридрих Энгельс и Владимир Ленин. О диалектическом материализме. – М.: Прогресс, 1977. – С. 305–306.

Процитировано в: Рукер «Четвертое измерение», с. 64.

Представим себе, что некий флатландец построил конструкцию из шести смежных квадратов, образующих подобие креста. С точки зрения флатландца, квадраты жестко соединены между собой. Из нельзя повернуть или иначе переместить относительно соединенных сторон. А теперь представим, что мы взяли эту конструкцию и решили отогнуть некоторые квадраты, чтобы образовался куб. Стыки между квадратами, жесткие в двумерном пространстве, в мире трех измерений легко поддаются, превращаясь в сгибы. Сложить куб настолько просто, что флатландец даже не заметит этого.

Но если флатландец очутится внутри куба, он обратит внимание на неожиданное явление. Каждый квадрат ведет в другой квадрат. «Внешней стороны» у куба нет. Всякий раз, когда флатландец переходит из одного квадрата в другой, он плавно, даже не замечая этого, сгибается под углом 90º в третьем измерении и попадает в следующий квадрат. Снаружи этот дом выглядит как самый обычный квадрат, но тот, кто войдет в него, обнаружит беспорядочное нагромождение квадратов, каждый из которых немыслимым образом ведет в следующий. Вошедшему покажется невероятным то, что этот единственный квадрат способен вместить шесть других квадратов.

Якоб Броновски «Восхождение человека» (Jacob Bronowski, The Ascent of Man, Boston: Little, Brown. 1974), с. 247.

Процитировано в: Абрахам Пайс «Научная деятельность и жизнь Альберта Эйнштейна» (Abraham Pais, Subtle Is the Lord: The Science and the Life of Albert Einstein, Oxford: Oxford University Press, 1982), с. 131.

Уравнения Максвелла выглядят так (мы принимаем с = 1):

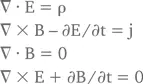
Вторая и последняя строчка – векторные уравнения, представляющие три уравнения каждое. Следовательно, всего уравнений Максвелла восемь.

Можно переписать их в релятивистской форме. Если ввести тензор Максвелла F μν= ∂ μ A ν – ∂ ν A μ, тогда уравнения сведутся к единственному:

Это и есть релятивистский вариант уравнений Максвелла.

Процитировано в: Абрахам Пайс «Научная деятельность и жизнь Альберта Эйнштейна», с. 239.

Процитировано в: Абрахам Пайс «Научная деятельность и жизнь Альберта Эйнштейна», с. 179.