Уолтер Левин - Глазами физика. От края радуги к границе времени

А это означало бы, что в какой-то момент толщина бедренных костей сравнялась бы с их длиной, а то и превысила бы ее, что закономерно сделало бы тело млекопитающего непропорциональным и слишком неуклюжим. Такое животное, конечно же, не имело бы шансов на выживание, чем, скорее всего, и объясняется ограничение максимального размера существующих млекопитающих.

Словом, мое предположение, что толщина кости должна увеличиваться быстрее ее длины. Тут-то и началось самое интересное.

Я отправился в Гарвардский университет, где хранится прекрасная коллекция костей животных, и попросил показать мне бедренную кость енота и лошади. Оказывается, лошадь примерно в четыре раза больше енота, и, соответственно, ее бедренная кость (42,0 ± 0,5 см) почти в три с половиной раза больше кости енота (12,4 ± 0,3 см). Пока все шло как надо. Подставив эти числа в свою формулу, я рассчитал, что бедренная кость лошади должна быть примерно в шесть раз толще кости енота. Я измерил толщину костей (с погрешностью около 0,5 сантиметра для енота и 2 сантиметра для лошади) и выяснил, что лошадиная кость в пять раз толще, плюс-минус около 10 процентов. Пока все говорило в пользу теории Галилео Галилея. Однако я решил расширить тест, включив в него более мелких и более крупных млекопитающих.

Я опять отправился в Гарвард, где мне показали еще три кости: антилопы, опоссума и мыши. Вот как они выглядели (плюс кость лошади):

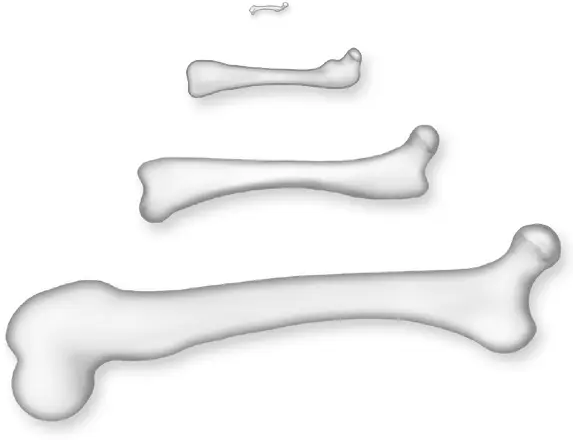
Ну разве это не прекрасно? Форма костей изменяется на удивление пропорционально; вы только поглядите, какая тоненькая и крошечная бедренная кость мыши! Малюсенькая и тонюсенькая бедренная косточка для малюсенькой мышки. Разве это не замечательно? Никогда не перестану поражаться красоте каждой детали матушки-природы.

Но как насчет результатов измерений, как они вписываются в мое уравнение? Произведенные расчеты повергли меня в шок, настоящий шок. Бедренная кость лошади оказалась примерно в 40 раз длиннее кости мыши и, согласно моим расчетам, в этом случае должна была быть более чем в 250 раз толще. А она была толще всего примерно в 70 раз.

И тут меня осенило: «А почему бы не попросить у них бедренную кость слона? Это помогло бы окончательно решить вопрос». Думаю, ребята в Гарварде были несколько раздражены, когда я явился к ним снова, но все же любезно выдали мне бедренную кость слона. К тому времени, я уверен, они просто хотели поскорее от меня избавиться! Поверьте, кость слона было очень трудно нести; она была длиннющая и, похоже, весила целую тонну. Я не мог дождаться момента, когда ее измерю, и не спал всю ночь.

И знаете, что я обнаружил? Бедренная кость мыши была 1,1 ± 0,05 см в длину и всего 0,7 ± 0,1 мм толщиной – действительно очень тонкая. Длина бедренной кости слона составляла 101 ± 1 см, то есть приблизительно в 100 раз длиннее кости мыши. А как насчет толщины? Измерив кость слона, я получил толщину 86 ± 4 мм, то есть примерно в 120 раз больше диаметра бедренной кости мыши. Однако, по моим расчетам, если Галилей прав, то бедренная кость слона должна была быть где-то в тысячу раз толще, чем у мыши. Иными словами, ее толщина должна составлять около 70 сантиметров. А на самом деле ее диаметр был где-то 9 сантиметров. В итоге мне пришлось признать, хоть и с крайней неохотой, что великий Галилео Галилей ошибался!

Одной из областей физики, для которой измерения стали истинным проклятием, является астрономия. Измерения и их погрешность – огромная проблема для астрономов, в частности потому, что дело приходится иметь с мегарасстояниями. Как далеко находятся звезды от Земли? Ну, например, наша прекрасная соседка Андромеда? А как насчет галактик, которые мы можем видеть только в самые мощные телескопы? Насколько далеки от нас наиболее удаленные объекты в космосе, которые мы видим? Насколько вообще велика наша Вселенная?

Это лишь некоторые из самых фундаментальных и глубоких вопросов всего естествознания. И разные ответы на них буквально перевернули наше представление о Вселенной с ног на голову. В сущности, у такого дела, как оценка астрономических расстояний, вообще замечательная история. Через изменения в методиках расчета расстояний до звезд можно проследить эволюцию самой астрономии. И на каждом этапе полученные данные зависят от степени точности измерений, то есть используемого оборудования и изобретательности астрономов. Например, вплоть до конца XIX века единственными данными, с помощью которых астрономы могли производить расчеты, был так называемый параллакс.

Вы все сталкивались с этим явлением, хотя чаще всего и не знали об этом. Где бы вы сейчас ни сидели, оглянитесь вокруг и найдите участок стены с каким-то элементом: дверным проемом или висящей картиной. А если вы находитесь на улице, то какой-нибудь заметный элемент ландшафта, например большое дерево. Теперь вытяните прямо перед собой руку и поднимите один из пальцев так, чтобы он оказался с той или другой стороны от выбранного вами объекта. Теперь зажмурьте сначала правый глаз, а затем левый. Вы увидите, как ваш палец перепрыгнет слева направо по отношению к дверному проему или дереву. Теперь переместите палец ближе к глазам и проделайте все снова. Ваш палец сместится еще сильнее. Эффект огромен ! Это и есть параллакс.

Все происходит из-за смены ракурса при наблюдении за объектом, в данном случае из-за перехода с линии зрения левого глаза на линию зрения правого (глаза человека расположены примерно в 6,5 сантиметра друг от друга).

Это и есть ключевая идея, лежащая в основе определения расстояний до звезд, только вместо 6,5 сантиметра, разделяющих наши глаза, в качестве базовой линии используется диаметр орбиты Земли (около 300 миллионов километров). По мере того как Земля обращается вокруг Солнца (по орбите с диаметром около 300 миллионов километров) в течение года, близлежащая звезда будет смещаться в небе относительно более удаленных звезд. Мы же раз в полгода измеряем угол в небе (угол параллакса) между двумя положениями этой звезды. Если произвести многократные измерения с полугодовым интервалом, получатся разные углы параллакса. На приведенном ниже рисунке я ради простоты примера выбрал звезду в плоскости орбиты Земли (так называемой орбитальной плоскости, или плоскости эклиптики), но описанный здесь принцип параллакса применим для любой звезды, а не только для звезд в плоскости эклиптики.

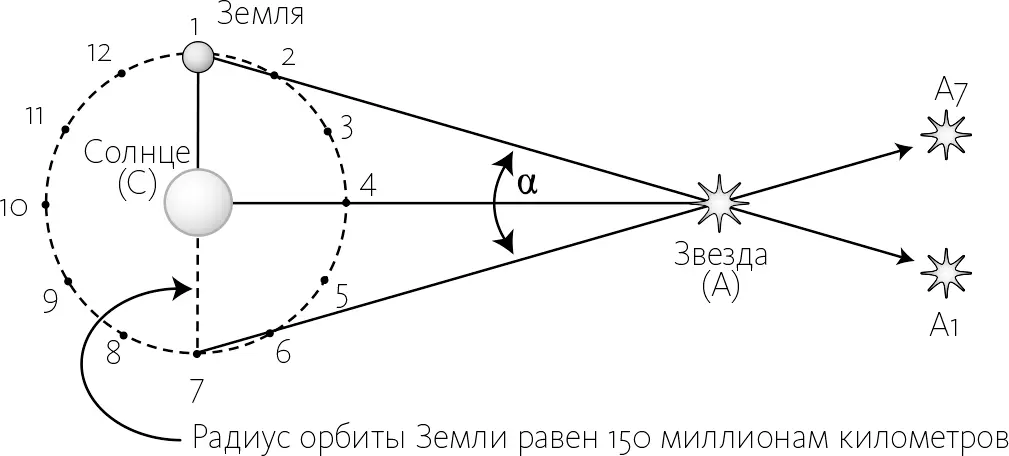
Предположим, вы наблюдаете звезду А в момент, когда Земля, двигаясь по орбите вокруг Солнца (С), находится в положении 1. В этом случае вы видите звезду проецируемой на фон (очень удаленный) в направлении A1. Если же вы наблюдаете ту же звезду шесть месяцев спустя (с позиции 7), то увидите ее в направлении A7. Угол, обозначенный как α, наибольший из всех возможных углов параллакса. Если произвести аналогичные замеры с позиций 2 и 8, 3 и 9, 4 и 10, углы параллакса всегда будут меньше, чем α. В гипотетическом варианте наблюдений из пунктов 4 и 10 (гипотетическом, потому что с позиции 10 звезду наблюдать невозможно, ибо мешает Солнце) угол параллакса вообще был бы равен нулю. А теперь посмотрите на треугольник, образуемый точками 1А7. Мы знаем, что расстояние 1–7 составляет 300 миллионов километров; нам также известно, что угол равен α. Следовательно, теперь можно без труда рассчитать расстояние CA (математика уровня средней школы).