Алексей Семихатов - Всё, что движется. Прогулки по беспокойной Вселенной от космических орбит до квантовых полей

Но неизвестными могут быть не только числа, но и более сложные объекты – функции. Пример функции – поведение (зависимость от времени) какой-либо величины, скажем объема вашего вклада в банке. Данные о том, что каждый день вклад увеличивается на 0,001 своей величины, являются, по существу, уравнением, из которого можно найти это поведение – функцию времени – и, например, узнать размер вклада через 1000 дней. Часто (хотя и не всегда) в задачах про такое поведение нет «зернистости» в виде фиксированного отрезка времени («дня»): считается, что функция изменяется непрерывно, и формулировка уравнений к этому приспособлена (такие уравнения называются дифференциальными, что примерно означает «имеют дело с очень малыми изменениями»). Пример поведения – координаты тела, движущегося в пространстве; чтобы задать его траекторию, требуются три функции времени – по одной для каждой из координат. Когда тела движутся под действием каких-либо сил, эти функции не произвольны, а определяются уравнениями движения.

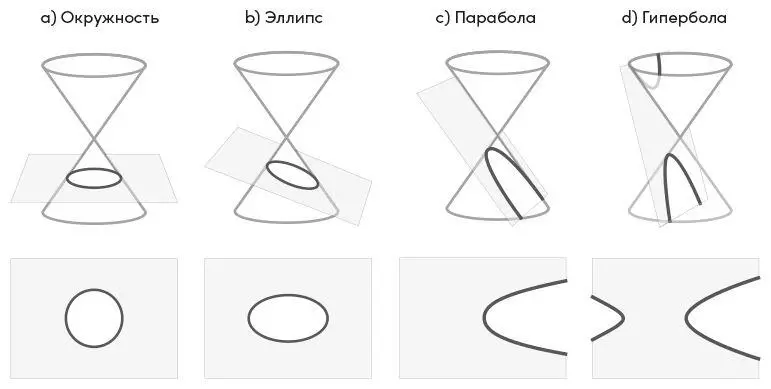
Рис. 1.7.Конические сечения

Уравнения, которые выражают законы природы, описывают точную (количественную) связь между какими-то величинами. Такие уравнения позволяют делать предсказания о поведении и свойствах изучаемых систем. Когда предполагается наличие в природе какой-либо связи, сопоставление предсказаний с наблюдениями служит для отбора тех уравнений, которые приводят к более точным предсказаниям. Несколько упрощая, можно сказать, что таким образом и формулируются работающие законы природы.

Конические сечения. Орбиты трех типов – эллипс (становящийся окружностью в частном случае), парабола и гипербола – объединены самим фактом того, что они и только они (кроме еще тривиального случая прямой линии) являются траекториями движения тел под действием притяжения одного центра. Они же объединены свойством совершенно иного типа: они и только они (и в специальном случае – прямая) возникают как пересечение плоскости и конуса. Конус – это поверхность, которая образуется, если свернуть в воронку лист бумаги, но с одним уточнением: математический конус продолжается по обе стороны от вершины, как видно уже на рис. 1.7 a . Если теперь пересечь конус плоскостью, которая перпендикулярна оси симметрии, то в сечении получится окружность. Наклоняя плоскость, мы получаем в сечении разнообразные эллипсы – всё более вытянутые по мере того, как наклон плоскости увеличивается (рис. 1.7 b ), – до тех пор, пока наклон не станет таким же, как наклон образующей конуса. В этом случае (рис. 1.7 c ) в сечении получается парабола (в некотором роде, как мы говорили, эллипсов много, а парабола одна; здесь эта идея выражается в том, что парабола возникает при точно обозначенном угле). Наклоняя плоскость еще сильнее, получаем в сечении гиперболы – разные в зависимости от угла наклона (рис. 1.7 d ). Здесь требуется небольшое пояснение: каждая гипербола имеет две части, потому что плоскость задевает и верхнюю, и нижнюю половины конуса. Говоря о гиперболе как о траектории движения, имеют в виду одну ее половину (которую тогда тоже называют гиперболой).

Почему три вида кривых, и только они, оказались решением двух столь различных задач (задача Кеплера и конические сечения) – вопрос, который нельзя было не задать некоторое число раз за те триста с лишним лет, как этот факт выяснился (конические сечения как таковые были известны в Древней Греции). Эллипс, кроме того, геометрически полностью симметричен относительно двух фокусов, что видно уже из построения с ниткой, показанного на рис. 1.1; но в Солнечной системе нет никакой «нитки», которая указывала бы планете, как двигаться, а сила действует на планету всегда и только в сторону одного из фокусов. Как же геометрия возникает из закона тяготения? Самый простой ответ: она получается как решение уравнений. Этот ответ, однако, никак не проясняет механизм, а из-за того, что уравнения здесь дифференциальные, он не относится к числу «элементарных». Есть ли элементарное решение, т. е. такое, которое позволяет перевести одну задачу (нахождение орбиты) в другую (построение конического сечения), причем делает это «непосредственно» и без использования математических средств типа дифференциального исчисления? Такое элементарное решение известно; в частности, ему посвящена «забытая» лекция Фейнмана – забытая на фоне других, прочитанных им в Калтехе и вошедших в «Фейнмановские лекции по физике». Однако Фейнман предваряет рассуждения таким предупреждением:

Элементарное вовсе не означает легкое для понимания. Элементарное означает, что для понимания не требуется почти никаких предварительных знаний, кроме бесконечно развитых умственных способностей.

Две «разные» параболы. Параболы оказались ответами в двух задачах: «планета» (частный случай движения вокруг центра притяжения, скажем Солнца) и «стрела», или, выразительнее, «камень» (движение, начинающееся под углом к горизонту вблизи земной поверхности). Одна и та же математическая кривая вполне может оказаться решением уравнений, записанных для различных систем, при разных предположениях. В задаче «планета» предполагается, что сила притяжения убывает при увеличении расстояния – «обратные квадраты», как это записано в (1.1). Парабола может тогда получиться в качестве решения при тщательно подобранных начальных условиях. В задаче «камень» предполагается другое: вблизи земной поверхности сила притяжения практически постоянна; поэтому можно спокойно пренебречь тем, как она убывает по мере подъема над поверхностью. В такой постановке задачи траектория брошенного тела – всегда парабола (разумеется, если убрать весь воздух – например, перенести эксперимент на Луну и там от души пострелять из рогатки), за очевидным исключением случаев бросания строго вверх и строго вниз. Если все же проявить дотошность и решить задачу про камень, не забывая, что притяжение ослабевает с высотой (и меняет направление по мере смещения вдоль земной поверхности!), то траектория от старта до падения окажется частью очень вытянутого эллипса – очень коротким отрезком его дуги вблизи его верхней части. На рис. 1.8 изображена часть эллипса, вытянутого несравненно слабее, чем тот, на который можно запустить камень любыми подручными средствами, но рисунок передает идею: небольшая дуга эллипса практически совпадает с параболой. Траекторией является только та часть каждой кривой, которая находится над поверхностью Земли, и, пока максимальная высота подъема мала по сравнению с радиусом планеты, участок эллипса неотличим от параболы. Поэтому вблизи поверхности Земли можно считать, что брошенные под углом к горизонту тела летят по параболе. Это Галилей и установил.