Марат Бурнашев - Ингенциальная математика. Монография

Сложение (1.1):

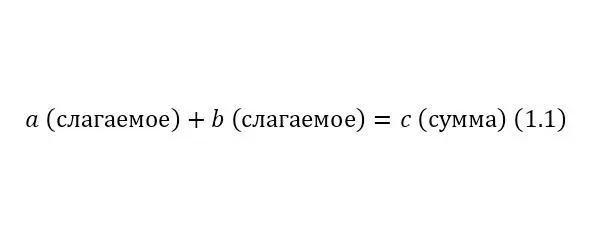
Умножение (1.2):

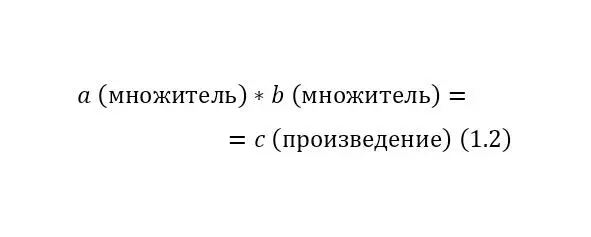
Вычитание (1.3):

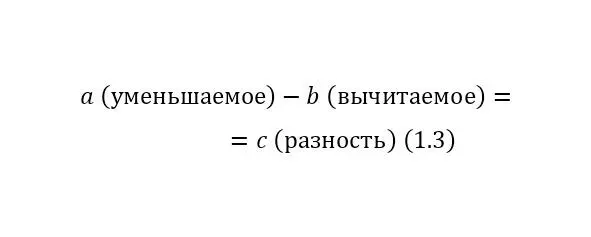
При этом уменьшаемое должно быть больше вычитаемого, иначе в результате получится отрицательное число или ноль, то есть число уже не будет принадлежать множеству натуральных чисел;

Деление (1.4):

Деление с остатком (1.5):

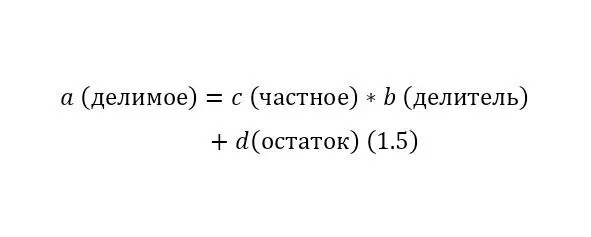
При этом сложение и умножение коммутативны и ассоциативны. А умножение дистрибутивно на сложении и вычитании.

Также можно перечислить и некоторые алгебраические операции:

Возведение в степень (1.6):

Также важно знать, что натуральные числа пишутся в ряд по возростанию.1, 2, 3, 4, 5, 6, 7 и т. д. Наименьшее натурально число – единица (1).

Класс – группа из трех цифр, на который разбито число, начиная справа. Последний класс может состоять из трех, двух или одной цифры. Первый класс – класс единиц; второй класс – класс тысяч; третий класс – класс миллионов; четвертый класс – класс миллиардов; пятый класс – класс триллионов; шестой класс – класс квадрильонов (квадриллионов); седьмой класс – класс квинтильонов (квинтиллионов); восьмой класс – класс секстильонов; девятый класс – класс септильонов и т.д.

Также имеют место числа вида:

1) Четные числа – это те числа, которые оканчиваются цифрами 0; 2; 4; 6; 8, то есть числа, которые делятся на 2 без остатка;

2) Нечетные числа – это те числа, которые оканчиваются цифрами 1; 3; 5; 7; 9 – числа не кратные 2.

Также по своей разновидности они делятся на 2 вида:

1) Простые числа – это натуральные числа, имеющие только два положительных делителя.

2) Составное число – это натуральное число, имеющее более двух положительных делителей.

Любое число, является либо простым, либо составным.

Целые числа – это натуральные числа, числа, противоположные им, и число нуль. Множество целых чисел обозначается буквой Z. Множество натуральных чисел входит в множество целых чисел, то есть является его подмножеством. Целые числа лежат на промежутке: (-∞; 0), то есть например: числа -1, -18, 0 – являются целыми. Над целыми числами можно проводить несколько алгебраических операций:

1) Сложение. Для того, чтобы сложить два целых числа с разными знаками, нужно из модуля большего числа вычесть модуль меньшего и перед результатом поставить знак большего по модулю числа.

2) Вычитание. Вычитание целых чисел сводится к сложению уменьшаемого и числа, противоположному вычитаемому.

3) Умножение. Для того, чтобы перемножить два целых числа, нужно перемножить их модули и перед произведением поставить знак плюс, если исходные числа были одного знака, и минус – если разного.

4) Деление. Для того, чтобы разделить одно целое число на другое, нужно разделить модуль первого числа на модуль второго и поставить перед частным знак плюс, если знаки делимого и делителя одинаковые, и минус, – если разные.

Целые числа делятся на 2 вида: положительные и отрицательные. Положительные целые числа – это целые числа больше нуля. Например, число 67 – целое число со знаком плюс, то есть положительное целое число большее нуля. На координатной прямой это число лежит справа от точки отсчета, за которую принято число 0. Другие примеры положительных целых чисел: 76,509, 87, 33, 12, 657.

Отрицательные целые числа – это целые числа меньшие нуля. Примеры целых отрицательных чисел: —987, —234, —1. Но стоит отметить, что само число (0) является не отрицательным и не положительным.

Любое число, противоположное положительному целому числу, в силу определения, является отрицательным целым числом. Справедливо и обратное. Число, обратное любому отрицательному целому числу, есть положительное целое число. Таким образом мы выяснили что (1.7).

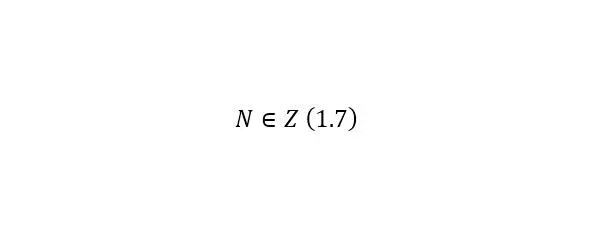
Рациональные числа – числа представимые в виде дроби k/m, где m≠ 0 и k – целое число, а m – натуральное число. Над рациональными числами можно проводить арифметические действия такие как: сложение, вычитание, умножение и деление (кроме деления на ноль). Обозначаются множество рациональных чисел буквой Q. Исходя из вышеперечисленных множеств можно сделать вывод что множество рациональных чисел охватывает два множества: натуральные и целые, то есть (1.8).

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.