Геннадий Ершов - Как рождается гравитация

Австрийский физик Й. Стефан показал, что суммарное излучение тела зависит только от его температуры и не зависит от природы самого вещества, из которого оно состоит.

Величина этой радиации прямо пропорциональна четвертой степени абсолютной температуры: то есть удвоение абсолютной температуры приводит к 16-кратному росту излучения, закон Стефана—Больцмана.

Вот она энергия, которая расширяет тела при их нагревании: каждый фотон (крафон) отщипывает квант энергии и создает квант импульса гравитации, оттягивающий оболочку тела по вектору своего полета. С повышением температуры спектр излучения смещается в коротковолновую область с повышением энергии каждого отлетающего кванта, соответственно, и повышением силы импульсов придачи.

Краткие выводы

• Теплота порождает фотонное излучение, которое увеличивает линейные размеры и объем тел.

• Расширение тел происходит под действием суммы импульсов излучения крафонов.

• С повышением температуры спектр излучения смещается в коротковолновую область с повышением энергии каждого отлетающего кванта, соответственно, и повышением силы импульсов придачи.

• В атоме в готовом виде нет фотонов, но в каждом физическом теле их бесчисленное количество.

• Земля в экваториальной области растягивается с помощью двух сил: центробежной силой и интегральной силой излучения.

2.8.1. Земля: эллипсоид вращения

Земля не сжимается на полюсах,

она расширяется на экваторе.

Земля – не шар, она имеет форму эллипсоида вращения, сплюснутого у полюсов. Для оценки сжатия Земли человечеству потребовалось немало усилий. А началось все это из-за расхождения хода часов. Француз Жан Рише в 1672 г. заметил, что его маятниковые часы, точно показывающие время в Париже, вдруг стали отставать на 2,5 минуты в сутки близ экватора в г. Кайенне (Французская Гвиана). Возникло подозрение, что почему-то полегчал груз, приводящий в движение механизм часов. Об этой истории стало известно Ньютону, который дал первую численную оценку величины сжатия Земли с учетом центробежной силы вращения. По его данным, разница между полярным и экваториальным радиусами должна составлять 1/230 долю от среднего радиуса. Эта оценка в течение почти столетия оставалась лучшей и наиболее обоснованной.

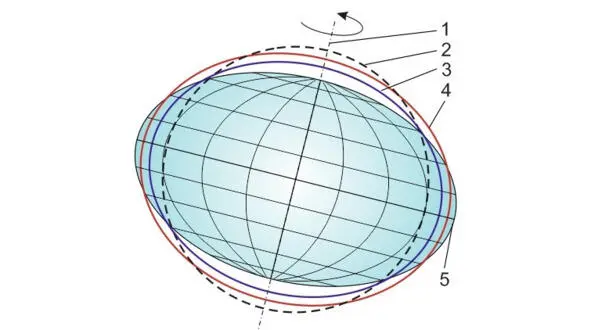
Рис. 2.7. Расширение Земли на экваторе. 1 – ось вращения, 2 – геоид, 3 – расширение за счет центробежной силы, 4 – расширение за счет электромагнитных сил излучения, 5 – расширение Земли.

Сжатие Земли экспериментально было подтверждено после обработки данных геодезических измерений двух французских экспедиций в Перу и Лапландию в 1730 г.

Исследованием фигуры Земли Занималось много ученых: Клеро, Пуанкаре, Лаплас, Лежандр, Стокс, Вихерт, Дарвин, Маклорен, Якоби и др. Было создано научное направление – теория фигур равновесия небесных тел.

Быстрое уточнение фигуры Земли началось с момента запуска искусственных спутников Земли. Сейчас величина сжатия вычислена довольно точно и в действительности равна 1/298.25.

Отношение разности большой экваториальной полуоси ( а ) земного эллипсоида и малой полярной полуоси ( b ) к большой полуоси, т. е. дробь: (a-b) /a называется сжатием Земли. Иногда это соотношение называют сплюснутостью Земли. Я не совсем согласен с признанным и устоявшимся в науке словосочетанием «сжатие Земли», на мой взгляд, более адекватным было бы словосочетание «расширение Земли». Земля не сжимается на полюсах, она расширяется на экваторе. За счет каких сил расширяется Земля, рассмотрим это явление подробнее.

2.8.2. Расширение Земли

Ньютон для определения сжатия Земли воспользовался моделью с двумя перпендикулярными сообщающимися скважинами (колодцами), пробуренными через центр Земли: одна – по оси вращения, другая – от экватора, и заполнил их водой. По логике, за счет центробежной силы вода в данных скважинах должна установиться на разных уровнях – в экваториальном колодце уровень воды должен быть выше. Во времена Ньютона не было практических данных измерения, сейчас эти данные есть, но они не согласуются с расчетными.

Приведу один из таких расчетов.

На тело массой m на поверхности Земли действует центробежная сила F c и сила тяжести F g .

M – масса Земли, R – ее радиус.

При этом угловая скорость будет равна:

Найдем отношение F c к F g для шарообразной Земли:

После подстановки значений и вычислений получим:

На экваторе любое тело должно весить примерно на 0,3% меньше, чем на полюсах. В действительности это различие не превышает 0,55% [6].

Можно воспользоваться другим способом вычисления, если приравнять вес каждого элементарного объема вещества на полюсе и на экваторе, при средней плотности Земли (5,52∙10 3 кг/м 3). Иначе, для равновесия на любом расстоянии r от центра Земли будет справедливо соотношение:

Зависимость ускорения свободного падения от радиуса в полярной и экваториальной скважинах одинаково:

где m – масса, заключенная внутри радиуса r .

ρ – плотность вещества, заполняющего скважины.

Если все это подставить в уравнение равновесия (2.14), сократить на m и проинтегрировать по всему радиусу Земли (левую часть – от 0 до полярного радиуса R p , правую – от 0 до экваториального радиуса R e ), то в результате получится соотношение:

Подставив в уравнение (2.16) среднюю плотность Земли 5,52 г/см 3и экваториальный радиус R e =6 378 140 м, получим R p ~6 367 140 м, т. е. полярный радиус должен быть меньше экваториального примерно на 11 км (в действительности – на 21 км), а отношение:

Величина f называется сжатием Земли, в действительности равна 1/298,257

Вычисления дают практически 50-процентное рассогласование с реальными измерениями. Тогда как это объяснить?

Поскольку геофизики не обнаружили никакой дополнительной силы, то находят объяснение в том, что: « Расчет плохо согласуется с реальной формой земной поверхности, поскольку мы не учитывали зависимость плотности от радиуса, а также – отличия реального распределения масс в недрах Земли от сферически-симметричного » [6].