Роджер Пенроуз - Большое, малое и человеческий разум

Рис. 1.1.

Рис. 1.2.

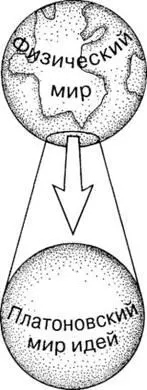
Я лично полагаю (и, мне кажется, большинство математиков и физиков-теоретиков придерживаются примерно той же точки зрения), что математика имеет другие, более серьезные основания и представляет собой некую структуру, управляемую собственными вневременными законами. Поэтому, возможно, многие физики и математики предпочли бы считать физический мир порождением «вневременного» математического мира идей. Соответствующая картина (рис. 1.3) при всей ее простоте очень важна для рассматриваемых в этой книге проблем (в особенности это относится к материалу гл. 3).

Рис. 1.3.

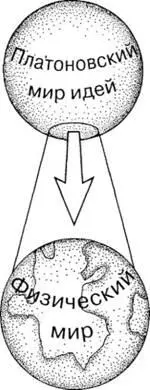
Наиболее замечательной характеристикой законов природы является то, что они подчиняются математическим закономерностям с исключительно высокой точностью. Чем глубже мы понимаем законы природы, тем сильнее чувствуем, что физический мир как-то исчезает, «испаряется», и мы остаемся лицом к лицу с чистой математикой, т. е. имеем дело лишь с миром математических правил и понятий.

Прежде чем перейти к дальнейшему рассмотрению, нам следует оценить временные и пространственные масштабы Вселенной и как-то связать их с местом и ролью человека в общей картине мира. Я сделал попытку объединить масштабы некоторых известных объектов и процессов в единую диаграмму (рис. 1.4), где слева представлены характерные времена, а справа — характерные размеры. В нижнем левом углу рисунка указан минимальный масштаб времени, имеющий какой-то физический смысл. Этот интервал времени, равный 10 -43с, называется планковским временем , или «хрононом», и он намного короче продолжительности всех известных нам процессов, включая очень краткие процессы физики элементарных частиц (например, время существования самых короткоживущих частиц-резонансов составляет около 10 -23с). Выше по диаграмме в логарифмическом масштабе указана длительность некоторых известных процессов, вплоть до возраста Вселенной.

Рис. 1.4. Характерное время и размеры некоторых объектов и процессов Вселенной.

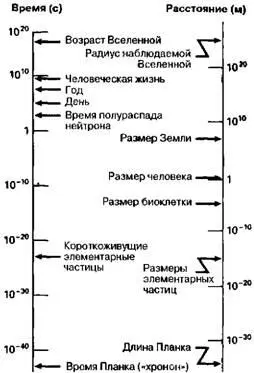
Справа на диаграмме приведены расстояния, соответствующие определенным временным масштабам. Времени Планка (хронону) соответствует фундаментальная единица, называемая планковской длиной . Две эти величины естественным образом возникают при любой попытке объединить физические теории, описывающие очень большие и очень малые объекты (речь идет об общей теории относительности Эйнштейна и квантовой механике). При любом сочетании вариантов этих теорий длина и время Планка выступают в качестве фундаментальных единиц измерения. Переход от левой шкалы диаграммы к правой осуществляется умножением на скорость света, что позволяет легко сопоставлять любой промежуток времени с расстоянием, проходимым световым сигналом за это время.

Размеры физических объектов на рисунке изменяются от 10 -15м (характерный размер элементарных частиц) до 10 27м (радиус наблюдаемой Вселенной, приблизительно соответствующий ее возрасту, умноженному на скорость света). Интересно оценить положение, которое на диаграмме занимаем мы , люди.

На шкале размеров мы находимся где-то в середине, будучи чрезвычайно крупными по отношению к длине Планка (и превышая на много порядков размеры элементарных частиц), но очень маленькими в масштабах всей Вселенной. С другой стороны, на временной шкале процессов длительность человеческой жизни выглядит совсем неплохо, и ее можно сопоставлять с возрастом Вселенной! Люди (и в особенности поэты) любят жаловаться на эфемерность человеческого существования, однако наше место на временной шкале вовсе не является жалким или ничтожным. Разумеется, нам следует помнить, что все сказанное относится к «логарифмической шкале», однако ее использование представляется совершенно оправданным при рассмотрении столь гигантских диапазонов значений. Говоря другими словами, число человеческих жизней, укладывающихся в возрасте Вселенной, намного меньше, чем число времен Планка (или даже времен жизни элементарных частиц), укладывающихся в продолжительность жизни человека. В сущности, мы являемся довольно стабильными структурами Вселенной. Что же касается пространственных масштабов, то мы действительно находимся где-то в середине шкалы, вследствие чего нам не дано воспринимать в непосредственных ощущениях ни очень большие, ни очень малые объекты окружающего нас физического мира.

Давайте рассмотрим, какие физические теории описывают объекты столь различных размеров. В схему рис. 1.5 я попытался «втиснуть» всю существующую физику. При этом мне, конечно, пришлось пожертвовать многими незначительными деталями (например, просто выкинуть из картины все уравнения и разделы наук!), однако, на мой взгляд, я сохранил фундаментальные теории.

Рис. 1.5.

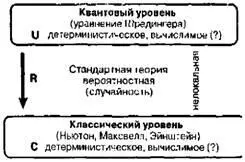
Наиболее существенным обстоятельством является то, что в физике используются два совершенно разных подхода. Для описания поведения микрообъектов мы используем квантовую механику (я обозначил ее на рисунке словами «квантовый уровень»), о которой подробнее рассказано в гл. 2. Большинство людей полагают, что квантовая механика является странной, загадочной и недетерминистической теорией, но это неверно. На самом деле, если вы рассматриваете события на квантовом уровне, то квантовая теория является совершенно точной и детерминистической. Наиболее известным ее соотношением является уравнение Шредингера, которое определяет поведение физического состояния квантовой системы (его называют просто квантовым состоянием ) и, безусловно, является совершенно точным и детерминистическим. Я использую букву U для обозначения всех расчетов или методов, связанных с квантовым уровнем рассмотрения. Неопределенность в квантовой механике возникает лишь тогда, когда вы осуществляете так называемое «измерение», требующее значительного «увеличения» масштаба события для перехода с квантового уровня на классический. Более подробно мы будем рассматривать эти проблемы в гл. 2.

При больших масштабах мы используем представления классической физики, которая является совершенно детерминистической. Она включает в себя законы механики Ньютона, законы Максвелла (позволяющие ввести в физику понятия электричества, магнетизма и света), две теории относительности Эйнштейна (специальную теорию относительности, описывающую движение тел при больших скоростях, и общую теорию относительности для систем с мощными гравитационными полями), причем все эти законы выполняются при больших расстояниях с исключительно высокой точностью.