Роджер Пенроуз - Большое, малое и человеческий разум

Рис. 1.16.

а— пространственно-временная картина расширяющейся Вселенной с евклидовыми пространственными сечениями (на рисунке указаны лишь два измерения), k= 0; б— пространственно-временная картина расширяющейся (а затем сжимающейся) Вселенной со сферическими пространственными сечениями, k= +1; в— пространственно-временная картина расширяющейся Вселенной с пространственными сечениями, описываемыми геометрией Лобачевского, k= -1; г— динамика развития трех указанных типов модели Фридмана.

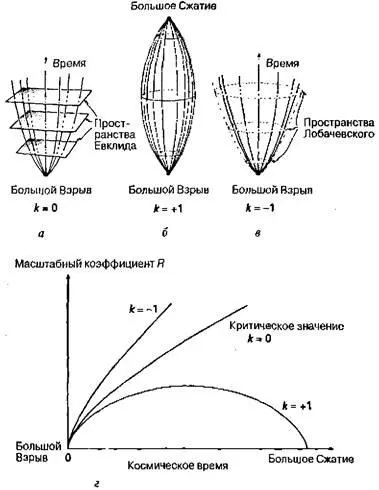
Полагая космологическую постоянную равной нулю, мы получаем для трех различных значений параметра k ( k = +1, 0, -1) три различные модели Вселенной (см. рис. 1.16). Разумеется, было бы правильнее учитывать также возраст и масштаб Вселенной (для этого необходимо пользоваться непрерывным, а не дискретным параметром k ), однако мы ограничимся лишь этими тремя моделями, поскольку их можно легко связать с кривизной пространственных сечений Вселенной. Если сечения являются плоскими, то этому соответствует нулевая кривизна и значение параметра k = 0 (рис. 1.16, а ). Если же сечения имеют положительную кривизну, то Вселенная является замкнутой и, следовательно, k = +1 (рис. 1.16, б ). В этих моделях Вселенная имеет сингулярное исходное состояние, знаменующее ее рождение (знаменитый Большой Взрыв). При k = +1 Вселенная после рождения расширяется (иногда говорят «раздувается») до некоторого максимального размера, после чего начинает сжиматься и «схлопывается» в момент Большого Сжатия. При k = -1 расширение Вселенной будет продолжаться вечно (рис. 1.16, в ), а случай k = 0 является промежуточным между двумя указанными. На рис. 1.16, г схематически показана зависимость радиуса Вселенной от времени, где под радиусом понимается некий характерный размер. Он может быть задан лишь при k = +1, а в двух остальных случаях Вселенная просто бесконечно расширяется.

Мне хочется подробнее рассмотреть случай с k = -1 (который, кстати сказать, труднее всего согласовать с общей картиной), представляющий интерес по двум важным причинам. Во-первых, эта модель наиболее удобна, если вы хотите трактовать результаты наблюдений по их истинному, «номинальному» значению. Дело в том, что в общей теории относительности искривление пространства обусловлено суммарным количеством вещества во Вселенной, а этого количества, по современным данным, явно недостаточно для создания Вселенной с замкнутой геометрией (разумеется, может оказаться и так, что Вселенная содержит большое количество так называемой скрытой, или темной, массы, которую мы еще просто не успели обнаружить, и тогда будет справедлива какая-то другая модель, однако, скорее всего, наша Вселенная не имеет столь большой массы и описывается параметром k = -1). Вторая причина моего интереса к этой модели связана с ее исключительной красотой и элегантностью.

На что похожи вселенные с параметром k = -1? Их пространственные сечения описываются так называемой гиперболической геометрией (геометрией Лобачевского), прекрасной иллюстрацией которой может служить одна из картин Мориса Эшера (рис. 1.17). Эшер нарисовал целую серию гравюр, озаглавленную «Предельные окружности», одна из которых и показана на рисунке. Как вы видите, художнику представляется, что Вселенная полна ангелов и чертей! Для нашего рассмотрения гораздо важнее то, что вся картина как бы выгнута по отношению к краям предельной окружности, и это искривление связано именно с попыткой художника изобразить гиперболическое пространство на плоском листе бумаги, иными словами — в привычном евклидовом пространстве. Следует осознать, что если бы мы жили в этой Вселенной, то форма и размеры всех чертей были бы одинаковы независимо от того, попали бы мы в центр или на край картины. Гравюра дает некоторое представление о том, что происходит в пространстве Лобачевского, и о тех особенностях, которые возникают при соответствующем искажении пространства.

Рис. 1.17. М. Эшер. «Предельная окружность 4» (представление геометрии Лобачевского).

Геометрия Лобачевского может показаться странной и неожиданной, но если вдуматься, то привычная нам евклидова геометрия — тоже совершенно замечательная вещь, хотя бы потому, что она дает нам прекрасные образцы взаимодействия физики и математики. Когда-то древние греки рассматривали ее не как раздел математики, а как описание окружающего мира.

Геометрия действительно описывает мир с поразительной точностью. Я говорю об очень высокой, но не абсолютной точности, поскольку, как мы уже видели, теория Эйнштейна доказала позднее, что наш мир в определенных условиях может быть «искривлен». Вопрос о возможности существования других геометрий всегда волновал ученых. Эта очень старая проблема известна под названием пятого постулата Евклида и сводится к справедливости утверждения о том, что через точку на плоскости, лежащую вне заданной прямой, можно провести только одну прямую, параллельную данной. Долгое время считалось, что это утверждение можно доказать, используя другие, более очевидные теоремы и положения евклидовой геометрии, однако позднее выяснилось, что такое доказательство невозможно, вследствие чего и возникло представление о неевклидовой геометрии.

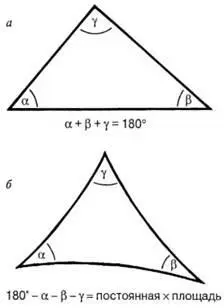
В такой геометрии сумма углов треугольника не равна 180°. На первый взгляд кажется, что это условие значительно усложняет рассмотрение, поскольку мы привыкли к тому, что в евклидовой геометрии сумма углов любого треугольника всегда составляет именно 180° (рис. 1.18, а ). Однако в неевклидовой геометрии разность между суммой углов треугольника и 180° пропорциональна площади треугольника, т. е. неожиданно выясняется, что площадь треугольника сложнее описать именно в евклидовой геометрии, где она задается сложным уравнением для всех углов и длин сторон треугольника. В неевклидовой геометрии площадь треугольника определяется замечательно простой формулой Ламберта (рис. 1.18, б ). Поразительно, но Ламберт вывел свою формулу до открытия неевклидовой геометрии!

Рис. 1.18.

а— треугольник в евклидовом пространстве; б— треугольник в пространстве Лобачевского.