Г. Шипов - Теория физического вакуума в популярном изложении

D pDx = const

Здесь Dxрассматривается как разброс координат точек внутри капли, а Dpкак разброс соответствующих им импульсов. Допустим, что капля принимает форму линии (вытягивается в линию), тогда ее импульс строго определен, поскольку разброс Dp= 0. Зато каждая точка линии становится равноправной, поэтому координата капли не определена из-за соотношения Dx= Ґ, которое следует из теоремы о сохранении фазового объема капли.

В теории поля для полевого сгустка, состоящего из набора плоских волн, теорема о сохранении фазового объема записывается в виде:

DpDx = p

где Dx- разброс координат полевого сгустка, а Dp- разброс волновых векторов плоских волн, образующих полевой сгусток. Если умножить обе части равенства на hи ввести обозначение р = h k, то мы получаем известное соотношение неопределенности Гейзенберга:

DpDx = p h

Это соотношение выполняется и для полевого сгустка, образованного набором плоских волн поля инерции в квантовой теории, следующей из теории физического вакуума.

Новая квантовая теория позволяет нам расширить наши представления об области действия квантовых явлений. В настоящее время считается, что квантовая теория применима только к описанию явлений микромира. Для описания таких макроявлений, как движение планет вокруг Солнца все еще используется представление о планете, как о пробной, не имеющей своего собственного поля, частице. Однако более точное описание движения планет достигается тогда, когда учитывается собственное поле планеты. Именно эту возможность предоставляет нам новая квантовая теория, использующая в качестве волновой функции в уравнении Шредингера поле инерции.

Таблица 3.

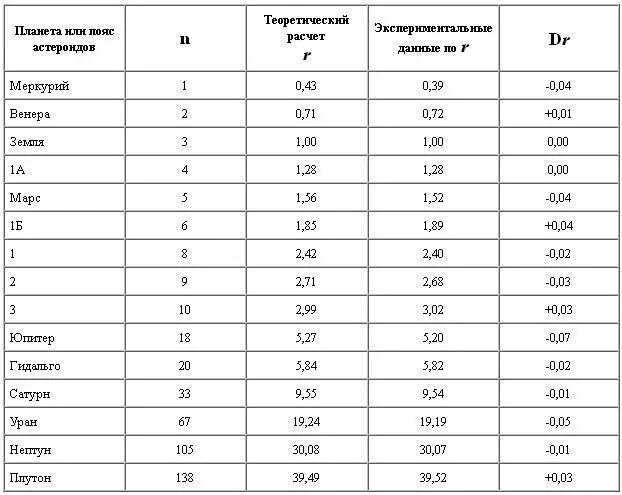
Простейшее квазиклассическое рассмотрение задачи движения планет вокруг Солнца с учетом их собственного поля приводит к формуле квантования средних расстояний от Солнца до планет (и астероидных поясов) по формуле:

r = r 0(n + 1/2), где n = 1, 2, 3 ...

Здесь r 0= 0,2851 а.е. = const - новая "планетарная константа". Напомним, что расстояние от Солнца до Земли равно 1 а.е. = 150000000 км. В таблице № 3 дано сравнение теоретических расчетов, полученных с помощью приведённой выше формулы, с результатами эксперимента.

Как видно из таблицы, вещество в Солнечной системе образует систему дискретных уровней, достаточно хорошо описываемых формулой, полученной из нового представления о природе волновой функции квантовой теории.

С древних времен было замечено, что форма предмета оказывает сильное воздействие на его восприятие. Этот факт относили к проявлению одной из сторон искусства в нашей жизни, придавая ему смысл субъективного эстетического видения реальности. Однако оказалось, что любой предмет создает вокруг себя "торсионный портрет", представляющий собой статическое (или динамическое) торсионное поле. Например, на рис. 17 изображено статическое торсионное поле конуса, помещенного в вакуум. Это поле создается формой конуса.

Для того чтобы убедиться в существовании торсионного поля, создаваемого конусом, был проведен эксперимент, изображенный на рис. 33 . В этом эксперименте перенасыщенный раствор соли КСl, находящийся в чашке Петри, был помещен над вершиной конуса. Одновременно такой же раствор находился в контрольной чашке, которая не подвергалась воздействию торсионного поля.

Рис. 33.Статическое торсиоиное поле конуса воздействует на процесс кристаллизации соли KCl

На рис. 34 представлены результаты эксперимента. Кристаллы соли в контрольном образце крупные и величина их различна. В середине облученного образца, куда попало торсионное излучение, кристаллы мелкие и более однородны.

Рис. 34. Результат воздействия торсионного поля на процесс кристаллизации соли KCL: а) - контрольный образец; б) - образец облученный торсионным полем.

В настоящее время российским ученым В.Т. Шкатовым создан прибор для измерения статических торсионных полей плоских изображений: геометрических фигур, букв, слов и текстов, а так же фотографий людей. На рис. 35 приведены результаты измерений статических торсионных полей некоторых плоских геометрических фигур, полученные с помощью торсиметра Шкатова.

Рис. 35.Результаты измерения торсионного контраста (ТК) плоских геометрических фигур: равностороннего треугольника, обратной свастики, пятиконечной звезды, квадрата, квадрата с петлями, прямоугольника с золотым соотношением сторон (соотношение сторон, равное D=1,618), креста с золотым соотношением, шестиконечной звезды, креста с фракталиями (т.е. с частями, подобными целому), прямой свастики и окружности.

Была разработана специальная методика, позволяющая определять интенсивность и знак (левое или правое) торсионного поля фигуры. На рис. 35 в нижней строке приведены значения измеренной торсионной контрастности, которая характеризует величину и знак торсионного поля фигуры по отношению к фону, в качестве которого выбиралось торсионное поле белого листа бумаги. Фигуры 5, 7, 8, 9, 10 и 11 создают правые торсионные поля, а 1, 2, 3, 4 левые.

Рис. 36. Измеренные с помощью торсиметра Шкатова значения торсионного контраста букв русского алфавита.

На рис. 36 представлены измерения торсионных полей, создаваемых буквами русского алфавита. Из этих данных видно, что буквы С и О, больше всего похожие на окружность, создают максимальный правый торсионный контраст, а буквы А и Ф максимальный левый. Прибор Шкатова позволяет измерять торсионный контраст отдельных слов, при этом ТК слова как правило равен сумме ТК букв, составляющих его. Иначе говоря, торсионное поле слова равно сумме торсионных полей составляющих его букв, правда это утверждение подтверждается с точностью 10-20%. Например, используя данные, представленные на рис. 36 , легко подсчитать, что ТК слова Христос равен +19.

После того, как было обнаружено, что торсионные поля могут изменять структуру кристаллов (см. рис 34 ), были проведены эксперименты по изменению кристаллической структуры металлов. Эти результаты впервые были получены украинским ученым В.П. Майбородой путем воздействия динамического излучения генератора Акимова на расплавленный металл, который плавился в печи Таммана. Схема экспериментальной установки представлена на рис. 37 .