Г. Шипов - Теория физического вакуума в популярном изложении

Из наших рассуждений можно прийти к выводу, что в геометризированной электродинамике возможно ускоренное движение по «инерции». Для этого заряженной частице достаточно двигаться согласно уравнениям геодезических пространства Римана. Причем это пространство должно быть образовано множеством относительных координат ускоренных локально инерциальных систем отсчета, связанных с зарядами. Поэтому в геометризированной электродинамике существование стационарных орбит электронов в поле ядра (квантовый принцип Бора) есть следствие ускоренного движения зарядов по инерции.

Этот вывод подтверждает догадки А. Эйнштейна о возможности найти более совершенную квантовую теорию путем расширения принципа относительности. В самом деле, появление стационарных орбит у электрона в геометризированной электродинамике обеспечено расширением специального принципа относительности электродинамики Максвелла-Лоренца-Эйнштейна до общего принципа относительности.

В повседневной жизни мы наблюдаем два типа движений тел - поступательные и вращательные. Например, автомобиль, который движется по горизонтальной поверхности, движется поступательно. Движение колес автомобиля относительно его корпуса является вращательным. Поступательное движение тел описывается в физике поступательными координатами х, у и z. Для описания вращательного движения используют вращательные координаты ф 1, ф 2, ф 3(ими могут быть углы Эйлера).

Механика Ньютона, электродинамика Максвелла-Лоренца-Эйнштейна, теория гравитации Эйнштейна и геометризированная электродинамика построены так, что используемые этими теориями системы отсчета образуют множество относительных поступательных координат (см. таблицу № 1 ). В таблице также указаны относительные физические величины, причем каждая более сложная теория включает в себя все предыдущие относительные величины и добавляет свои. Например, в электродинамике Максвелла-Лоренца-Эйнштейна, которая использует четырехмерные инерциальные системы отсчета, кинетическая энергия равномерного движения зарядов относительна, так же как и в механике Ньютона. Но в ней дополнительно оказываются относительными длина объекта и время его жизни. В теории гравитации Эйнштейна и геометризированной электродинамике относительно все то, что и в электродинамике Максвелла-Лоренца-Эйнштейна, плюс относительными оказываются гравитационные и электромагнитные поля соответственно.

Таблица № 1.

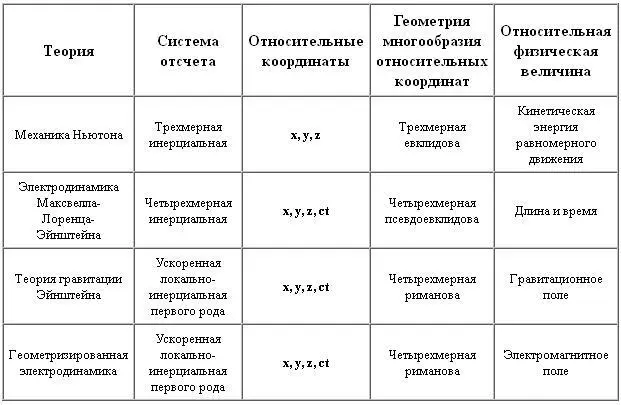
Легко видеть, что в эту таблицу не входят вращательные координаты ф 1, ф 2, ф 3. Это и понятно, поскольку все перечисленные в таблице системы отсчета по определению не вращаются. Поэтому можно сказать, что до сих пор теория относительности развивалась как теория поступательной относительности.

Следующий шаг в развитии теории относительности потребовал введения многообразия относительных координат ускоренных систем отсчета, которые испытывают вращение при своем движении. Такие системы отсчета движутся не только в трансляционных координатах, но также и во вращательных. Теория, в которой используются вращательные координаты, требует увеличения размерности пространства событий. Например, если рассматриваются трехмерные вращающиеся системы отсчета с трансляционными координатами х, у и z, то они дополнительно описываются тремя вращательными координатами. В этом случае пространство событий шестимерно. Если же мы будем рассматривать четырехмерные вращающиеся системы отсчета, то пространство событий будет уже десятимерным, поскольку в четырехмерном пространстве трансляционных координат х, у, z, ct имеется шесть вращательных координат: три пространственных угла ф 1, ф 2, ф 3и три псевдоевклидовых угла q 1, q 2, q 3.

Трансляционные и вращательные координаты существенно отличаются по своим свойствам. Трансляционные координаты относятся к классу голономных (или интегрируемых). Движение в голономных координатах характерно тем, что оно не зависитот направления пути в одну и ту же точку пространства.

Рис. 8.Результат движения в голономных координатах х, у,и zне завит от последовательности пути движения.

Наглядно это свойство изображено на рис. 8, где показано движение в голономных координатах х, у, и zиз начала координат О до точки Р по отрезкам 1, 2 и 3 вдоль осей Ох, Оу и Oz. Ha рис. 8 а) движение начинается вдоль оси хна величину отрезка 1, затем вдоль оси уна величину отрезка 2 и, наконец, вдоль оси zна величину отрезка 3. В результате мы приходим в точку Р. На рис. 8 б) порядок движения изменился: сначала движение происходит вдоль оси уна величиау отрезка 2, затем вдоль оси хна величину отрезка 1 и, окончательно, вдоль оси zна величину отрезка 3. И опять мы приходим в точку Р. Этот же результат мы получим, если начнем движение вдоль оси z, как это показано на рис. 8 в).

В отличие от голономных координат х, у, и z, при движении в неголономных координатах ф 1, ф 2, ф 3результат двух поворотов на конечные углы зависит от последовательности этих поворотов. Для иллюстрации этого утверждения, рассмотрим два последовательных поворота вокруг осей х, и z на углы 90° (рис. 9 и 10).

Рис. 9.Два последовательных поворота на угол 180°:а) - поворот на 90°по часовой стрелке вокруг оси z; б) - то же, вокруг оси у; в) - результат двух последовательных поворотов.

Рис. 10.Смена порядка последовательных поворота на угол 180°: а) -поворот на 90°по часовой стрелке вокруг оси у, б) - то же, вокруг оси z; в) - результат двух последовательных поворотов.

Из рисунков видно, что результат двух конечных поворотов вокруг осей у и z зависит от последовательности этих поворотов (положения квадрата со звездочкой на рис. 9 в и рис. 10 в не совпадают).

Самый простой пример вращательного движения представляет собой вращающийся диск.

Рис. 11. На центр масс однородного вращающегося диска по всем направлениям действуют скомпенсированные центробежные силы инерции. По определению, такая система представляет собой ускоренную локально-инерциальную систему отсчета второго рода.