Кудрявцев Степанович - Курс истории физики
- Название:Курс истории физики
- Автор:
- Жанр:
- Издательство:Просвещение
- Год:1982
- Город:Москва
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Кудрявцев Степанович - Курс истории физики краткое содержание
Курс истории физики предназначен для студентов педагогических институтов. В нём изложена история мировой физики от древности до наших дней. Книга состоит из трёх частей. В первой освещена история становления физической науки, заканчивающейся Ньютоном. Последняя, третья часть посвящена истории становления квантовой, релятивисткой и ядерной физики.
Курс истории физики - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
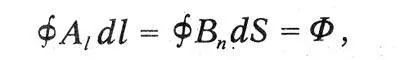
где A - компонента вектора потенциала
в направлении элемента кривой dl, Bn ~ нормальная компонента вектора индукции В в направлении нормали к элементу поверхности dS.
Далее Максвелл пишет «уравнение магнитной проводимости»:
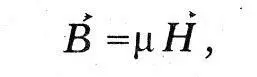
связывающее магнитную индукцию В с вектором напряженности магнитного поля Н.
Третий закон связывает напряженность магнитного поля Н с силой создающего ее тока I. Максвелл формулирует его так: «Полная магнитная интенсивность вдоль линии, ограничивающей какую-нибудь часть поверхности, служит мерой количества электрического тока, протекающего через эту поверхность». В современных обозначениях это предложение описывается формулой
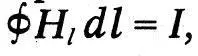 ,
,
которая ныне называется первым уравнением Максвелла в интегральной форме. Она отражает экспериментальный факт, открытый Эрстедом: ток окружен магнитным полем.
Четвертый закон — это закон Ома:
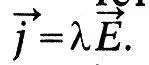
Для характеристики силовых взаимодействий токов Максвелл вводит величину, называемую им магнитным потенциалом. Эта величина подчиняется пятому закону: «Полный электромагнитный потенциал замкнутого тока измеряется произведением количества тока на полную электротоническую интенсивность вдоль цепи, считаемую в направлении тока:
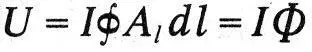 ».
».
Шестой закон Максвелла относится к электромагнитной индукции: «Электродвижущая сила, действующая на элемент проводника, измеряется производной по времени от электротонической интенсивности, независимо от того, обусловлена ли эта производная изменением величины или направления электротогмческого состояния». В современных обозначениях этот закон выражается формулой:
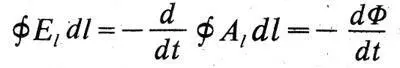
представляющей собой второе уравнение Максвелла в интегральной форме. Заметим, что электродвижущей силой Максвелл называет циркуляцию вектора напряженности электрического поля. Максвелл обобщает закон индукции фарадея — Ленца— Неймана, считая, что изменение во времени магнитного потока (электротонического состояния) порождает вихревое электрическое поле, существующее независимо от того, есть ли замкнутые проводники, в которых это поле возбуждает ток, или нет. Обобщения же закона Эрстеда Максвелл пока не дает.
формулировку шести законов Максвелл заканчивает следующими словами: «Я сделал попытку дать в этих шести законах математическое выражение той идеи, которая, по моему мнению, лежит в основе хода мыслей фарадея в его «Экспериментальных исследованиях». Это утверждение Максвелла совершенно справедливо, как справедливо и другое утверждение, что введение «математических функций для выражения фарадеевского электротонического состояния и для определения электродинамических потенциалов и электродвижущих сил» сделано им впервые.
Следующий шаг в развитии теории электромагнитного поля Максвелл сделал в 1861—1862 гг., опубликовав ряд статей под общим заглавием «О физических силовых линиях». И здесь Максвелл прибегает к механической модели электромагнитного поля. Но эта модель значительно сложнее, чем картина поля скоростей движущейся жидкости, которую он разрабатывал в предыдущей работе. Максвелл разрабатывал эту модель, используя в полной мере свой талант механика и конструктора, и пришел к своим знаменитым уравнениям. «Максвелл,—писал Больцман, — нашел свои уравнения в результате стремления доказать при помощи механических моделей возможность объяснения электромагнитных явлений, исходя из концепции близко действия, и только эти модели впервые указали путь к тем экспериментам, которые окончательно и решительно установили факт близко-действия и в настоящее время образуют наиболее простой и наиболее достоверный фундамент найденных другим путем уравнений».
Найти уравнения Максвелла нетрудно, но «вывести» их невозможно, так же как невозможно вывести законы Ньютона. Конечно, и уравнения Ньютона и уравнения Максвелла могут быть выведены из других принципов, которые приходится принимать без доказательства, но эти принципы, как и сами уравнения Максвелла или Ньютона, представляют собой обобщения опыта. «Теория Максвелла — это уравнения Максвелла»,— сказал Герц.
В «физических линиях силы» Максвелл прежде всего обосновывает выражение силы, действующей на каждый элемент среды, в которой находятся заряды, токи, магниты. Максвелл мыслит среду заполненной молекулярными вихрями, силы, действующие в этой среде в одной и той же точке, зависят от направления, они носят, как мы теперь говорим, тензорный характер. Далее Максвелл записывает свои знаменитые уравнения. Новым по сравнению с работой о фарадеевских линиях силы здесь является четкое установление связи между изменениями магнитного поля и возникновением электродвижущей силы. Его уравнение (точнее, «триплет» уравнений для компонентов) определяет «отношения между изменениями состояния магнитного поля и электродвижущими силами, ими обусловленными».
Другой важной новостью является введение понятий смещения и токов смещения. Смещение, по Максвеллу,— это характеристика состояний диэлектрика в электрическом поле. Полный поток смещения через замкнутую поверхность равен алгебраической сумме зарядов, находящихся внутри поверхности. «Это смещение, — пишет Максвелл,—не представляет собой настоящего тока потому, что, достигнув определенной величины, оно остается постоянным. Но это есть начало тока, и изменения смещения образуют токи в положительном или отрицательном направлении в зависимости от того, увеличивается смещение или уменьшается». Так вводится фундаментальное понятие тока смещения. Этот ток, так же как и ток проводимости, создает магнитное поле. Поэтому Максвелл обобщает то уравнение, которое ныне называется первым уравнением Максвелла, и вводит в первую часть ток смещения. В современных обозначениях это уравнение Максвелла имеет вид:
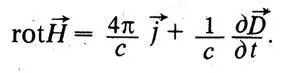
Интервал:
Закладка:









