Лев Ландау - Физика для всех. Молекулы

В настоящее время известна структура около сотни белковых молекул. Работа продолжается. Всего в живом организме имеется около десятка тысяч различных белков. От того, как они свернуты и в каком порядке следуют друг за другом разные аминокислотные остатки, зависит деятельность живого организма. Нет сомнения, что работа по определению структуры белковых молекул будет продолжаться до тех пор, пока не будет получена полная ясность в отношении всех десяти тысяч сортов молекул, определяющих жизненные процессы.

На рис. 9.3 мы привели фотографию одного из вирусов. О структуре этой частицы, пожалуй, стоит сказать несколько слов, так как вирусы.- это простейшие "живые" частицы. Они представляют собой комплексы белков и нуклеиновых кислот. Сами же белки и нуклеиновые кислоты относят к биоорганическим молекулам. Назвать эти молекулы "живыми" было бы неверно.

Белок и нуклеиновая кислота комбинируются в вирусе так, чтобы глобулы защищали нуклеиновую кислоту. Эта защита может осуществляться двумя способами. Либо глобулы образуют полый цилиндр, внутрь которого прячется нуклеиновая кислота, либо глобулы составляют полый шар, а нуклеиновая кислота располагается внутри полости.

Каковы размеры вирусов? Вот, скажем, вирус табачной мозаики. Его длина 3000 Å, внешний диаметр 170 Å, диаметр канала 80 Å. В вирус входит 2140 молекул белка.

Поражает исключительная упорядоченность расположения молекул белка, образующих оболочку вируса. Все белковые молекулы свернуты в глобулы абсолютно тождественным образом. Строго закономерна и упаковка глобул.

Сферические вирусы близки к шару по своей форме. Однако на самом деле представляют собой высокосимметричные многогранники, известные геометрам под названием икосаэдров.

Трудно переоценить значение для науки структурных исследований простейших живых веществ для молодой науки - молекулярной биологии.

Если молекулы могут хорошо упаковаться, будучи предельно растянуты, то твердый полимерный материал может образовать разные довольно сложные структуры, обладающие, однако, одним общим свойством. В той или иной степени в твердом теле будут присутствовать участки, в которых молекулы примыкают друг к другу, как карандаши в пачке.

В зависимости от того, каков в теле процент таких пачечных участков, а также смотря по тому, сколь аккуратно упакованы молекулы, составляющие пачечный участок, полимер может обладать тем или иным "процентом кристалличности". Большинство полимеров противятся простой классификации твердых тел на аморфные и кристаллические. Удивительного в этом ничего нет, поскольку речь идет об огромных, да ещё вдобавок чаще всего неодинаковых молекулах. Упорядоченные ("кристаллические") участки в полимерах можно грубо разбить на три класса: пачки, сферолиты и кристаллы из складывающихся молекул.

Типичная микроструктура полимера показана на рис. 9.4. Это фотоснимок с увеличением в 400 раз, сделанный с пленки полипропилена. Звездообразные фигурки - это своего рода кристаллиты. Из центра звездочки при охлаждении полимера начался рост сферолита. Затем сферолиты встретились и поэтому не приобрели идеальной сферической формы (если удается наблюдать за ростом отдельного сферолита, то действительно видишь шар, так что название "сферолит" вполне оправдано). Внутри сферолита длинные молекулы уложены достаточно аккуратно. Скорее всего, сферолит можно представить себе как аккуратно сложенный канат. Роль каната играет пачка молекул. Таким образом, своей длинной осью молекулы расположены перпендикулярно к радиусу сферолита. На той же фотографии мы видим пластичные участки. Возможно, это пачки молекул, а может быть, и кристаллы из складывающихся молекул. Существование подобных кристаллов является интересным и достоверным фактом, относящимся к структуре линейных полимеров.

Рис. 9.4

Двадцать лет назад было сделано следующее замечательное открытие. Из раствора были выделены кристаллики различных полимерных веществ. Исследователи были поражены тем, что такие же кристаллики, поверхности которых похожи на спиральную лестницу, вырастали из растворов различных парафинов. В чем же причина этого спирального роста кристаллов, напоминающего результаты труда искусного кондитера (рис. 9.5)?

Рис. 9.5

Говоря о росте кристалла на стр. 99, мы обошли одно обстоятельство. Представим себе, что строящаяся плоскость кристалла заполнена атомами. Тогда не остается мест, которые притягивали бы атомы достаточно сильно. Можно подсчитать, что по такой схеме рост должен идти со скоростями, в немыслимое число раз меньшими, чем скорости роста, наблюдаемые в действительности. Выход из положения дает наличие спиральных дислокаций в кристалле. Если есть спиральная дислокация, то наращивание грани идет таким образом, что ступеньки, на которых атомам выгодно занять место, никогда не зарастут. Физики облегченно вздохнули, когда были обнаружены спиральные дислокации. Им стали понятны величины скоростей роста и стала очевидной суть картинок, подобных приведенной выше для парафина. Такие спиральные пирамидки наблюдаются очень часто, и в том, что они существуют, нет ничего удивительного. Нет удивительного, если речь идет о кристаллах, построенных из малых молекул. Для таких кристаллов объяснение проходит: размер молекулы, высота ступеньки, толщина кристалла - все эти данные не противоречат друг другу.

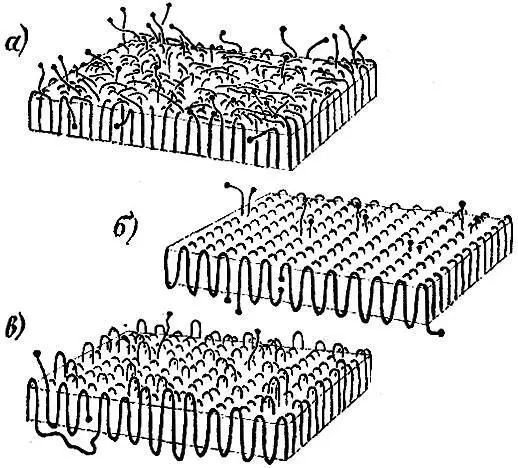
Но, обнаружив такую же картинку для полимера, мы сталкиваемся с новым явлением. Дело в том, что толщина слоев полиэфира равна 100-120 Å, а длина молекулы равна 6000 Å. Какой же вывод можно сделать из этих цифр? Да всего лишь один - в этих кристалликах молекулы складываются. Гибкость молекул позволяет им изогнуться без труда, и поэтому остается лишь раздумывать (раздумывание продолжается и до сих пор), какая из трех моделей, показанных на рис. 9.6, лучше. Различие между ними, конечно, второстепенное. Впрочем, специалист обидится. "Как же второстепенное,- скажет он,- на верхнем снимке молекулы загибаются, как попало, минуя ближайших соседей, на второй модели при сворачивании молекула становится соседкой самой себе. Различие между второй и третьей моделью заключается в том, что на среднем рисунке поверхность кристалла более гладкая, чем на нижнем".