Яков Перельман - Межпланетные путешествия. Полёты в мировое пространство и достижение небесных тел

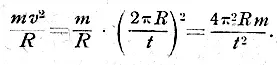
С другой стороны, центростремительная сила должна быть равна силе взаимного притяжения обращающихся тел — иначе кругового движения не могло бы быть. Эта сила выражается формулой

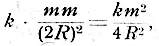
где k — „постоянная тяготения", т-е. 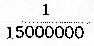дины.

Приравнивая оба выражения:

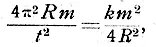
определяем из этого равенства величину t , т.-е. продолжительность обращения:

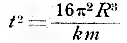
откуда

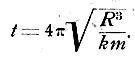
Подставляя для нашего случая вместо R -100 см., m — 65.000 и зная, что π = 3,14,

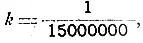
имеем:

Следовательно, время обращения двух человеческих тел, кружащихся под действием силы взаимного тяготения по круговой орбите с диаметром 2 метра, равно 190.284 сек., или 53,6 часа (около двух суток) [29] Если время обращения и диаметр орбиты известны, то можно вычислить, по той же формуле, неизвестные массы обращающихся тел. Так определяют астрономы массы двойных звезд. .

Как вычислить время взаимного падения тяготеющих друг к другу тел, — показано далее, в статье „Падение в мировом пространстве".

В заключение приводим интересный отрывок, характеризующий силу тяготения и заимствуемый у известного английского физика О. Лоджа [30] „Мировой эфир", гл. IX. :

„Силы тяготения между небольшими телами незначительны и далеко превосходятся магнитными. Действительно, притяжение между телами определенной малости может быть более чем уравновешено даже давлением, возникающим вследствие их взаимного излучения, несмотря на то, что это давление почти бесконечно мало. Отсюда следует, что достаточно малые тела любой температуры отталкивают друг друга (если только они не заключены в оболочку постоянной температуры, где лучистое давление на них со всех сторон одинаково).

Размеры, при которых лучистое отталкивание перевешивает тяготение, в случае двух равных шаров, зависят от температуры шаров и от их плотности; по данным проф. Пойтинга, при обыкновенной, привычной для нас температуре— скажем, при 16° Ц. — равенство этих двух сил для двух деревянных шаров, расположенных в пространстве, достигается тогда, когда каждый шар имеет диаметр приблизительно в один фут. Для тел меньших размеров или более горячих лучистое отталкивание пересиливает взаимное тяготение; отталкивание это возрастает пропорционально четвертой степени абсолютной температуры тел.

Притягательная сила тяготения между молекулами чрезвычайно мала; между двумя атомами или двумя электронами она настолько мала, что ею можно пренебречь, хотя бы расстояние между ними и не выходило из пределов размера молекулы.

А между тем, от совокупного притяжения мириад таких тел происходит результирующая сила тяготения, заметная на расстояниях в миллионы миль. Сила эта не только заметна, но величину ее нужно признать прямо-таки ужасающей.

Когда дело идет о телах астрономических размеров, сила тяготения перевешивает все другие силы; и все электрические и магнитные притяжения в сравнении с нею падают до полного ничтожества".

„Все сделанные попытки объяснить силу тяжести, как результат движения в среде, находящейся между телами, наталкиваются на то затруднение, что тяжесть беспрепятственно проходит сквозь тела, как бы велики и плотны они ни были, — пишет Аррениус [31] Аррениус, „Физика неба". . — Так, например, притяжение Солнца действует на частицу, лежащую в центре Земли, сквозь все промежуточные слои. А так как действие силы должно состоять в каком-нибудь изменении движения тела, подвергающегося ее влиянию, то необходимо принять, что частица, лежащая позади другой, подверженной той же силе, по крайней мере отчасти закрыта от этого влияния. Поэтому на соединительной линии между частицею в центре Земли и любою частицею на Солнце не должна была бы лежать ни одна из бесконечно большого числа тяжелых частиц верхних слоев Земли. Значит, необходимо предположить, что частицы, на которые действует сила тяжести, имеют бесконечно малое протяжение и должны считаться математическими точками. Физически этот взгляд немыслим. Точно также невозможно представить себе, чтобы математические точки могли возмущать движение. Удивительно, что та самая сила природы, которую мы точнее всего можем проследить посредством вычисления, в физическом отношении представляет величайшую загадку".

Совершенно особым образом подходит к вопросу новейшая (1915 г.) теория тяготения, разработанная А. Эйнштейном, которая вовсе не рассматривает тяготение как некоторую „силу". Исходным пунктом теории тяготения Эйнштейна являются следующие соображения [32] Приводимый далее отрывок заимствован из книги проф. О. Д. Хвольсона „Теория относительности А. Эйнштейна и новое миропонимание" (Пг., 1922). :

„Вообразим себе систему в виде большого ящика или комнаты и положим сперва, что она находится в гравитационном поле, т. е. в такой части пространства, в которой действуют силы тяготения, и что она в этом пространстве неподвижна. В виде примера представим себе, что она находится на земной поверхности, где гравитация, т. е. сила тяжести, действует вертикально вниз от потолка к полу комнаты. Наблюдатели, находящиеся в этой системе, заключают следующее. Тела, спокойно лежащие на полу, на столе и т. д., производят давление на тела, находящиеся под ними. Если взять в руку какое-либо тело, напр., свинцовый шарик, и отпустить его, то он начинает падать вертикально вниз с ускорением, которое мы обозначим буквой g , и которое оказывается независящим от рода тела, если исключить сопротивление воздуха. Если шарик бросить в горизонтальном направлении, то он начнет двигаться по кривой линии (по параболе) вниз, и на некотором расстоянии от наблюдателя достигнет пола. В обоих случаях мы имеем дело с весомой массой взятого тела.