Александр Китайгородский - Физика для всех. Движение. Теплота

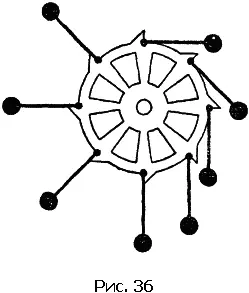
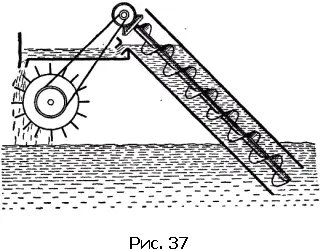
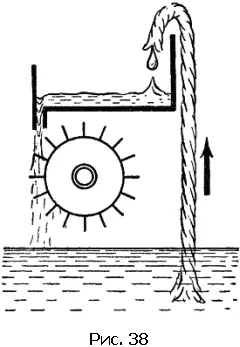
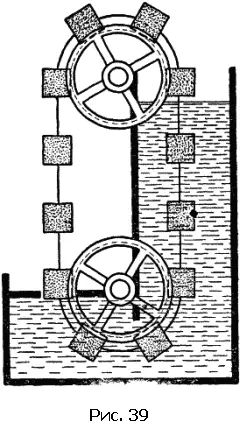
Вариантов предлагавшихся вечных двигателей было в общем немного: разнообразные самодвижущиеся колеса, в принципе не отличающиеся от описанного, гидравлические двигатели – например, показанный на рис. 37 двигатель, изобретенный в 1634 г.; двигатели, использующие сифоны или капиллярные трубки (рис. 38), потерю веса в воде (рис. 39), притяжение железных тел магнитами. Далеко не всегда можно догадаться, за счет чего же должно было, по идее изобретателя, происходить вечное движение.

Еще до установления закона сохранения энергии утверждение о невозможности перпетуум мобиле мы находим в официальном заявлении французской Академии, сделанном в 1775 году, когда она решила не принимать больше для рассмотрения и испытания никакие проекты вечных двигателей.

Многие механики XVII–XVIII веков уже клали в основу своих доказательств аксиому о невозможности перпетуум мобиле, несмотря на то, что понятие энергии и закон сохранения энергии вошли в науку много позже.

В настоящее время ясно, что изобретатели, которые пытаются создать вечный двигатель, не только входят в противоречие с экспериментом, но и совершают ошибку против элементарной логики. Ведь невозможность перпетуум мобиле есть прямое следствие из законов механики, из которых они же исходят, обосновывая свое «изобретение».

Несмотря на полную бесплодность, поиски вечного двигателя, вероятно, сыграли все же какую-то полезную роль, так как в конечном счете привели к открытию закона сохранения энергии.

При всяком столкновении двух тел всегда сохраняется импульс. Что же касается энергии, то она, как мы только что выяснили, обязательно уменьшится из-за различного рода трения.

Однако, если сталкивающиеся тела сделаны из упругого материала, например из кости или стали, то потеря энергии будет незначительной.

Такие столкновения, при которых суммы кинетических энергий до и после столкновения одинаковы, называются идеально упругими.

Небольшая потеря кинетической энергии происходит и при столкновении самых упругих материалов – у костяных биллиардных шаров она достигает, например, 3–4 %.

Сохранение кинетической энергии при упругом ударе позволяет решить ряд задач.

Рассмотрим, например, лобовое столкновение шаров разной массы. Уравнение импульса имеет вид (мы считаем, что шар № 2 покоился до удара)

m 1 v 1= m 1 u 1+ m 2 u 2,

а энергии –

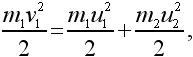
где v 1– скорость первого шара до столкновения, а u 1и u 2– скорости шаров после столкновения.

Так как движение происходит вдоль прямой линии (проходящей через центры шаров – это и означает, что удар лобовой), то применять векторные обозначения здесь не обязательно.

Из первого уравнения имеем:

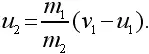
Подставляя это выражение для u 2в уравнение энергии, получим:

Одним из решений этого уравнения является решение u 1= v 1и u 2= 0. Но этот ответ нас не интересует, так как равенства u 1= v 1и u 2= 0 означают, что шары вовсе не сталкивались. Поэтому ищем другое решение уравнения.

Сократив на m 1( v 1− u 1), получим:

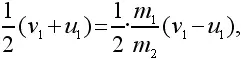
т.е.

m 2v 1+ m 2u 1= m 1v 1− m 1u 1

или

( m 1− m 2) v 1= ( m 1+ m 2) u 1,

что дает следующее значение для величины скорости первого шара после удара:

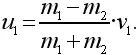
При лобовом столкновении с неподвижным шаром налетающий шар отскакивает обратно ( u 1отрицательно), если его масса меньше. Если m 1больше m 2, то оба шара продолжают движение в направлении удара.

При биллиардной игре в случае точного лобового удара часто наблюдается такая картина: шар-снаряд резко останавливается, шар-мишень отправляется в лузу. Это объясняется только что найденным уравнением. Массы шаров равны, и уравнение дает u 1= 0, а значит, u 2= v 1. Налетающий шар останавливается, а второй шар начинает движение со скоростью налетевшего. Шары как бы меняются скоростями.

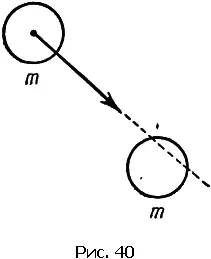
Рассмотрим еще один пример столкновения тел по закону упругого удара, а именно косой удар тел равной массы (рис. 40). Второе тело до удара покоилось, поэтому законы сохранения импульса и энергии имеют вид:

mv 1= mu 1+ mu 2,

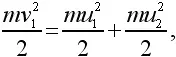
Сократив на массу, получим:

v 1= u 1+ u 2, v 1 2= u 1 2+ u 2 2.

Вектор v 1есть векторная сумма u 1и u 2. Но ведь это означает, что длины векторов-скоростей образуют треугольник.

Что же это за треугольник? Вспомним теорему Пифагора. Ее выражает наше второе уравнение. Это значит, что треугольник скоростей должен быть прямоугольным с гипотенузой v 1и катетами u 1и u 2. Значит, u 1и u 2образуют между собой прямой угол. Этот интересный результат показывает, что при любом косом упругом ударе тела равной массы разлетаются под прямым углом.

В некоторых случаях равновесие очень трудно поддержать – попробуйте пройтись по натянутому канату. В то же время никто не награждает аплодисментами сидящего в кресле-качалке. А ведь он тоже поддерживает свое равновесие.

В чем же разница в этих двух примерах? В каком случае равновесие устанавливается «само собой»?

Условие равновесия как будто бы очевидно. Чтобы тело не смещалось из своего положения, действующие на него силы должны уравновешиваться; иными словами, сумма этих сил должна равняться нулю. Это условие действительно необходимо для равновесия тела, но достаточно ли оно?