Александр Китайгородский - Физика для всех. Движение. Теплота

Замена параллельных сил одной равнодействующей – задача, осуществимая всегда (за исключением одного особого случая, о котором будет сказано в конце этого параграфа). Рассмотрим сложение параллельных сил. Конечно, сумма сил в 3 кГ и 5 кГ равна 8 кГ, если силы смотрят в одну сторону. Задача состоит в том, чтобы найти точку приложения (линию действия) равнодействующей.

На рис. 54 изображены две действующие на тело силы. Суммарная сила F заменяет силы F 1и F 2, но это значит не только то, что F = F 1+ F 2, действие силы F будет равноценно действию F 1и F 2в том случае, если и момент силы F будет равен сумме моментов F 1и F 2.

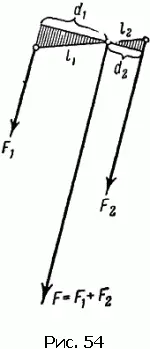
Мы ищем линию действия суммарной силы F . Конечно, она параллельна силам F 1и F 2, но на каких расстояниях проходит эта линия от сил F 1и F 2?

В качестве точки приложения силы F на рисунке изображена точка, которая лежит на отрезке, соединяющем точки приложения сил F 1и F 2. По отношению к выбранной точке момент F , разумеется, равен нулю. Но тогда сумма моментов F 1и F 2по отношению к этой точке тоже должна равняться нулю, т.е. моменты сил F 1и F 2, противоположные по знаку, будут равны по величине.

Обозначив буквами d 1и d 2плечи сил F 1и F 2, можем записать это условие так:

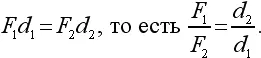
Из подобия заштрихованных треугольников следует, что d 2/ d 1= l 2/ l 1, т.е. точка приложения суммарной силы на соединительном отрезке делит расстояние между складываемыми силами на части l 1и l 2, обратно пропорциональные силам.

Обозначим буквой l расстояние между точками приложения сил F 1и F 2. Очевидно, l = l 1+ l 2.

Решаем систему двух уравнений с двумя неизвестными:

F 1 l 1− F 2 l 2= 0,

l 1+ l 2= l.

Получим:

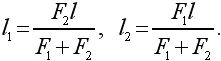
По этим формулам мы можем найти точку приложения равнодействующей силы не только в том случае, когда силы смотрят в одну сторону, но и в случае с силами, направленными в противоположные стороны (как говорят, антипараллельными). Если силы направлены в разные стороны, то они имеют противоположные знаки, и равнодействующая равна разности сил F 1− F 2, а не их сумме. Считая отрицательной меньшую из двух сил F 2, видим по нашим формулам, что l 1становится отрицательным. Это значит, что точка приложения силы F 1лежит не левее (как ранее), а правее точки приложения равнодействующей (рис. 55), при этом по-прежнему

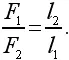
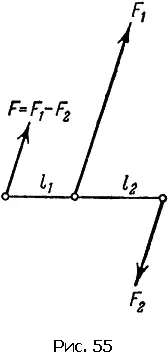
Интересный результат получается при равных антипараллельных силах. Тогда F 1+ F 2= 0. Формулы показывают, что l 1и l 2становятся при этом бесконечно большими. Какой же физический смысл имеет это утверждение? Так как относить результирующую в бесконечность бессмысленно, то, значит, равные антипараллельные силы нельзя заменить одной. Такую комбинацию сил называют парой сил.

Действие пары сил нельзя свести к действию одной силы. Любые две параллельные или антипараллельные силы можно уравновесить одной, а пару сил – нельзя.

Разумеется, было бы неверным сказать, что силы, составляющие пару, уничтожают одна другую. Пара сил оказывает весьма существенное действие – вращает тело; особенность действия пары сил состоит в том, что она не дает поступательного движения.

В некоторых случаях может возникнуть вопрос не о сложении параллельных сил, а о разложении данной силы на две параллельные.

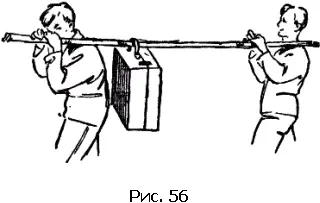
На рис. 56 изображены два человека, которые вместе несут на палке тяжелый чемодан. Вес чемодана раскладывается на обоих. Если груз давит на середину палки, то они оба испытывают одинаковую тяжесть. Если расстояние от точки приложения груза до рук, которые его несут, d 1и d 2, то сила F разложится на силы F 1и F 2по правилу

Кто сильнее, тот должен взяться за палку поближе к грузу.

Все частички тела обладают весом. Поэтому твердое тело находится под действием бесчисленного количества сил тяжести. При этом все эти силы параллельны. Если так, то их можно сложить по правилам, которые мы только что рассматривали, и заменить одной силой. Точка приложения суммарной силы называется центром тяжести. В этой точке как бы сосредоточен вес тела.

Подвесим тело за одну из его точек. Как оно при этом расположится? Поскольку мы можем мысленно заменить тело одним сосредоточенным в центре тяжести грузом, ясно, что в равновесии этот груз будет лежать на вертикали, проходящей через точку опоры. Другими словами, в равновесии центр тяжести лежит на вертикали, проходящей через точку опоры, и находится в самом низком положении.

Можно расположить центр тяжести на вертикали, проходящей через ось, и над точкой опоры. Это удастся сделать с большим трудом и только благодаря наличию трения. Такое равновесие неустойчиво.

Мы уже говорили об условии устойчивого равновесия – потенциальная энергия должна быть минимальна. Так оно и есть в том случае, когда центр тяжести лежит ниже точки опоры. Любое отклонение повышает центр тяжести и, значит, увеличивает потенциальную энергию. Напротив, когда центр тяжести лежит над точкой опоры, то любое дуновение, выводящее тело из этого положения, ведет к уменьшению потенциальной энергии. Такое положение неустойчиво.

Вырежем из картона фигуру. Для того чтобы найти центр ее тяжести, подвесим ее два раза, приклеивая нитку-подвес сначала в одной, а потом в другой точке тела. Закрепим фигуру на оси, проходящей через центр тяжести. Повернем фигуру в одно положение, второе, третье… Мы обнаружим полное безразличие тела к нашим операциям. В любом положении осуществляется специальный случай равновесия. Его так и называют – безразличным.

Причина этого ясна – при любом положении фигуры заменяющая ее материальная точка находится в одном и том же месте.

В ряде случаев центр тяжести можно найти и без опыта и вычислений. Ясно, например, что центры тяжести шара, круга, квадрата, прямоугольника находятся в центрах этих фигур, так как они симметричны. Если мысленно разбить симметричное тело на частички, то каждой из них будет соответствовать другая, расположенная симметрично по другую сторону от центра. А для каждой пары таких частиц центр фигуры явится центром тяжести.