Александр Китайгородский - Физика для всех. Движение. Теплота

Значит, земной слой, находящийся над телом, все равно что отсутствует. Действие отдельных его частей на тело уравновешивается, и суммарная сила притяжения со стороны внешнего слоя равняется нулю.

Конечно, во всех этих рассуждениях мы считали плотность Земли постоянной внутри каждого слоя.

Результат наших рассуждений позволяет легко получить формулу для силы тяжести, действующей на любой глубине H под землей. Точка, расположенная на глубине H , испытывает лишь притяжение со стороны внутренних слоев Земли. Формула для ускорения силы тяжести g = γ( M / R ) применима и для этого случая, но M и R – это масса и радиус не всей Земли, а ее «внутренней» по отношению к этой точке части.

Если бы Земля имела одинаковую плотность во всех слоях, то формула для g приняла бы вид:

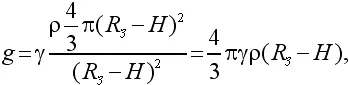
где ρ – плотность, R З– радиус Земли.

Это значит, что g менялось бы прямо пропорционально ( R З– H ): чем больше глубина H , тем меньше было бы g .

На самом же деле поведение g вблизи земной поверхности – мы можем проследить за ним вплоть до глубин 5 км (ниже уровня моря) – совсем не подчиняется этому закону. Опыт показывает, что в этих слоях g , наоборот, растет с глубиной. Расхождение опыта с формулой объясняется тем, что не было учтено различие плотности на разных глубинах.

Средняя плотность Земли легко находится делением массы на объем земного шара. Это приводит нас к цифре 5,52. В то же время плотность поверхностных пород много меньше – она равна 2,75. Плотность земных слоев растет с глубиной. В поверхностных слоях Земли этот эффект берет верх над идеальным уменьшением, которое следует из выведенной формулы, и величина g возрастает.

На простом примере мы уже познакомились с энергией тяготения. Тело, поднятое на высоту h над землей, обладает потенциальной энергией mgh .

Однако этой формулой можно пользоваться лишь тогда, когда высота h много меньше радиуса Земли.

Энергия тяготения – важная величина, и интересно получить формулу ее, которая годилась бы для тела, поднятого на любую высоту над землей, а также вообще для двух масс, притягивающихся по универсальному закону:

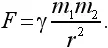
Положим, что под действием взаимного притяжения тела немного сблизились. Между ними было расстояние r 1, а стало r 2. При этом совершается работа A = F ( r 1– r 2). Значение силы надо взять в какой-то средней точке. Итак,

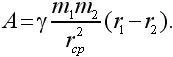
Если r 1и r 2мало отличаются друг от друга, то можно заменить r ср 2произведением r 1 r 2. Получаем:

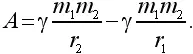
Эта работа произведена за счет энергии тяготения:

A = U 1− U 2,

где U 1– начальное, а U 2– конечное значение потенциальной энергии тяготения.

Сопоставляя эти две формулы, находим для потенциальной энергии выражение

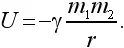
Оно похоже на формулу силы тяготения, но в знаменателе стоит r в первой степени.

По этой формуле при очень больших r потенциальная энергия U = 0. Это разумно, так как на таких расстояниях притяжение уже не будет чувствоваться. Но при сближении тел потенциальная энергия должна уменьшаться. Ведь за ее счет происходит работа.

А куда же уменьшаться от нуля? В отрицательную сторону. Поэтому в формуле и стоит минус. Ведь −5 меньше нуля, а −10 меньше −5.

Если речь идет о движении около земной поверхности, то общее выражение силы тяготения можно заменить произведением mg . Тогда с большой точностью U 1− U 2= mgh .

Но на поверхности Земли тело имеет потенциальную энергию −γ( Mm / R ), где R – радиус Земли. Значит, на высоте h над земной поверхностью

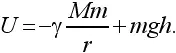
Когда мы впервые ввели формулу потенциальной энергии U = mgh , было условлено высоту и энергию отсчитывать от земной поверхности. Пользуясь формулой U = mgh , мы отбрасываем постоянный член −γ( Mm / R ), условно считаем его равным нулю. Так как нас интересуют лишь разности энергий – ведь обычно измеряется работа, которая есть разность энергий, – то присутствие постоянного члена −γ( Mm / R ) в формуле потенциальной энергии роли не играет.

Энергия тяготения определяет прочность цепей, «привязывающих» тело к Земле. Как порвать эти цепи, как добиться того, чтобы брошенное с Земли тело не вернулось на Землю? Ясно, что для этого нужно придать телу большую начальную скорость. Но каково же минимальное требование?

По мере отдаления от Земли потенциальная энергия выброшенного с Земли тела (снаряда, ракеты) будет расти (абсолютное значение U падает); кинетическая энергия будет падать. Если кинетическая энергия тела станет равной нулю преждевременно, до того как мы оборвем цепи тяготения земного шара, выброшенный снаряд упадет обратно на Землю.

Необходимо, чтобы тело сохраняло кинетическую энергию до тех пор, пока его потенциальная энергия практически не упадет до нуля. Перед отправлением снаряд обладал потенциальной энергией −γ( Mm / R ) ( M и R – масса и радиус Земли). Поэтому снаряду нужно дать такую скорость, которая сделала бы полную энергию оторвавшегося снаряда положительной. Тело с отрицательной полной энергией (абсолютное значение потенциальной энергии больше значения кинетической) не выберется за пределы сферы тяготения.

Таким образом, мы приходим к простому условию. Для того чтобы тело массы m оторвать от Земли, надо, как уже сказано, преодолеть потенциальную энергию тяготения

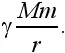
Скорость снаряда должна быть при этом доведена до значения так называемой второй космической скорости v 2, которую легко вычислить из равенства кинетической и потенциальной энергий:

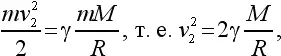
или, так как g = γ( M / R 2),

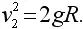
Значение v 2, вычисляемое по этой формуле, составляет 11 км/с, – конечно, без учета сопротивления атмосферы. Эта скорость в sqrt(2) = 1,41 раза больше первой космической скорости v 1= sqrt( g R) искусственного спутника, вращающегося около земной поверхности, т.е. v 2= sqrt(2)· v 1.