Юн Эльстер - Объяснение социального поведения. Еще раз об основах социальных наук

При моделировании дисконтирования во времени специалисты по теории принятия решений традиционно предполагают, что люди дисконтируют будущую прибыль экспоненциально (exponentially). Одна единица прибыли t периодов в будущем имеет настоящую ценность k t , где k < 1 является коэффициентом дисконта на этот период. Экспоненциальное дисконтирование привлекательно, с нормативной точки зрения, тем, что позволяет осуществлять последовательное планирование (consistent planning). Если один поток вознаграждений имеет в данный момент времени бо́льшую ценность, чем другой, он будет иметь бо́льшую настоящую ценность во всех временных точках. Следовательно, у агента никогда не происходит инверсия предпочтений (preference reversal), которая обычно (в отсутствие причин для пересмотра решения) рассматривается как знак иррациональности.

Однако эмпирически понятие последовательного планирования не имеет особого смысла. Случайное наблюдение показывает, а систематическое подтверждает, что у большинства из нас часто возникает инверсия предпочтений. Очень часто мы не в состоянии последовать намерениям экономить, делать зарядку по утрам, заниматься на фортепьяно, не опаздывать на встречи и так далее. Я могу позвонить дантисту 1 марта и записаться к нему на 1 апреля только затем, чтобы потом отменить запись 30 марта, сказав (солгав), что должен идти на похороны. Чтобы объяснить эти разновидности повседневной иррациональности (а также многие другие явления), мы можем заменить предположение об экспоненциальном дисконтировании гиперболическим дисконтированием (hyperbolic discounting).

Предположим, что дисконтированная настоящая ценность 1 единицы прибыли t периодов в будущем равна 1 / (1 + k t ) (в приведенном ниже примере я принимаю k = 1, но в более общем случае k может быть любым положительным числом: чем оно больше, тем меньше агента заботит будущее). Более того, предположим, что агент при t = 0 сталкивается с выбором: вознаграждение 10 при t = 5 и вознаграждение 30 при t = 10. При t = 0 настоящая ценность первого составляет 1,67, а у послед-него она равна 2,73. У агента, который максимизирует настоящую ценность, сформируется намерение выбрать отложенное вознаграждение. При t = 1 настоящая ценность более быстрой награды равняется 2, более поздней – 3. При t = 2 эти значения составляют соответственно 2,5 и 3,3; при t = 3 они составляют 3,3 и 3,75; и при t = 4 они равняются 5 и 4,29. В какой-то момент между t = 3 и t = 4 скорейшее вознаграждение перестает быть крайней опцией и становится более предпочтительной только в результате того, что идет время . Действительно, легко увидеть, что переключение происходит при t = 3,5; именно тогда я звоню своему дантисту, чтобы отменить встречу.

Еще лучше эта модель видна на графике. На рис. VI.3 агент может выбрать или небольшое вознаграждение Б при t 1 или дождаться t 2 и получить большее вознаграждение А . Гиперболические кривые I и II представляют то, как оцениваются значения этих вознаграждений в разные предшествующие моменты. По сути они являются кривыми безразличия (глава IX), которые представляют компромиссы между временем получения вознаграждения и размером этого вознаграждения. К примеру, в момент t агенту все равно, получить вознаграждение PQ немедленно или получить небольшое вознаграждение на t 1, а также ему все равно, получить PR немедленно или получить большую награду в момент t 2. Поскольку во момент t настоящая ценность у А больше, чем у Б , она сформирует намерение выбрать А . Однако поскольку гиперболические кривые пересекаются в t* , в этот момент возникает инверсия предпочтений и агент выбирает Б вместо этого [97].

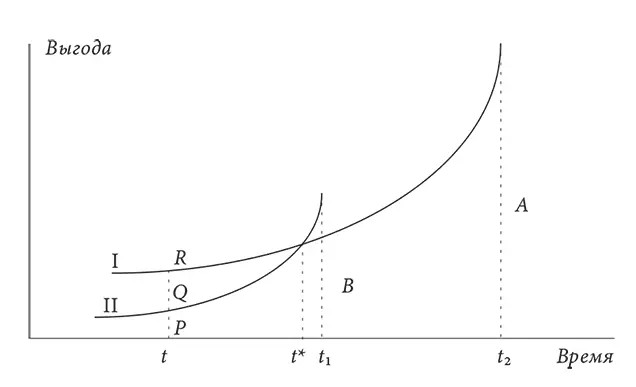
РИС. VI.3

Мы можем использовать паскалевское пари, чтобы проиллюстрировать отношения между экспоненциальным и гиперболическим дисконтированием во времени. Паскаль хотел убедить своих друзей, свободомыслящих игроков, в том, что они должны поставить на Бога, поскольку даже самая малая вероятность вечного блаженства компенсирует величайшие земные удовольствия. В аргументе Паскаля заключено много сложностей, некоторые из которых мы рассмотрим в следующей главе. Здесь я хочу привлечь внимание к вопросу, который Паскаль не упоминает: имеет настоящая (дисконтированная) ценность вечного блаженства конечную или бесконечную ценность? Если она конечна, игрок может предпочесть получить свои удовольствия на земле, вместо того чтобы ждать загробной жизни.

Предположим для простоты, что каждый период загробной жизни дает 1 единицу прибыли; что человек, по его предположениям, умрет через n число лет от настоящего момента; и наконец, что он дисконтирует будущее благосостояние по экспоненте с множителем k (0 < k < 1). Если Бог дарует человеку спасение по вере его, настоящая ценность блаженства в первый год после его смерти составит k n единиц прибыли, во второй год k n + 1и так далее. Если следовать элементарной алгебре, эта бесконечная сумма ( k n + k n + 1 + k n + 2…) складывается с конечной суммой k n/ 1 – k . Можно представить по крайней мере, что эта сумма может быть меньше настоящей ценности n лет гедонистической жизни на земле. Наоборот, если агент подвержен гиперболическому дисконтированию, бесконечная сумма 1 / ( n + 1) + 1 / ( n + 2) + 1 / ( n + 3) … увеличивается, выходя за пределы любой данной конечной ценности, предполагая, что если мы сравним настоящие ценности, любые земные удовольствия будут в конечном счете заслонены блаженством спасения. Даже если последнее будет умножено на сколь угодно малую вероятность того, что Бог существует, результат по-прежнему будет перерастать пределы любого конечного числа.

Предположим, однако, что собеседник Паскаля имеет возможность регулярно играть в азартные игры. Предварительно рассмотрев ситуацию, он предпочитает пойти к мессе, а не поиграть, потому что первая заставит его поверить и обещает ему вечное блаженство. Однако, по логике гиперболического дисконтирования, имманентная возможность играть в азартные игры вызывает инверсию предпочтений. У него появится намерение сыграть еще один раз, а затем начать ходить к мессе. Вслед за блаженным Августином он скажет: «Дай мне целомудрие и воздержание, но не сейчас». Однако на следующей неделе он рассудит таким же образом. Так сама структура дисконтирования во времени, обеспечивающая более высокую настоящую ценность вечного блаженства, помешает игроку предпринять шаги для его достижения.