Донелла Медоуз - Пределы роста. 30 лет спустя

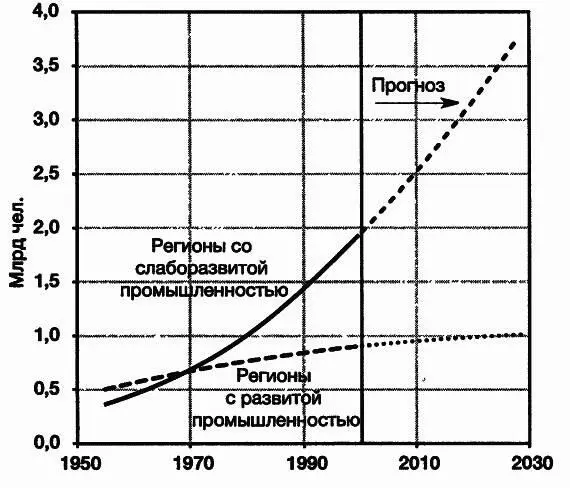
Рис. 2.2.Городское население в мире

За прошедшие 50 лет городское население экспоненциально увеличивалось в странах со слаборазвитой промышленностью и практически линейно — в промышленно развитых странах. Среднее время удвоения городского населения в странах со слаборазвитой промышленностью составляет 19 лет. Предполагается, что этот показатель сохранится в ближайшие несколько десятилетий. (Источник: UN.)

постоянный период времени всегда одинаково, оно не зависит от того, каким было само значение параметра в этот момент.

Величина растет экспоненциально, если приращение пропорционально самой величине. Колония дрожжей, в которой каждая клетка делится на две каждые 10 минут, растет экспоненциально. Из каждой клетки через 10 минут будет уже 2 клетки. Еще через 10 минут их будет уже 4, еще через 10 минут — 8, затем 16 и т. д. Чем больше клеток, тем больше новых клеток образуется в единицу времени. Прибыль компании, которая успешно увеличивает валовую выручку на определенный процент в год, через несколько лет экспоненциально вырастет. Когда параметр растет экспоненциально, приращение тоже растет с течением времени, оно зависит от того, каково значение самого параметра в этот момент.

Ключевое отличие экспоненциального роста от линейного можно проиллюстрировать на примере. Допустим, у вас есть 100 долларов. Вы можете положить деньги в банк и получать проценты (вклад с капитализацией процентов) или положить их в копилку и каждый год добавлять определенную сумму. Если вы внесли на счет 100 долларов под 7 % годовых с капитализацией, то есть добавлением процентов к сумме счета, то вклад будет расти экспоненциально. Каждый год сумма будет прирастать

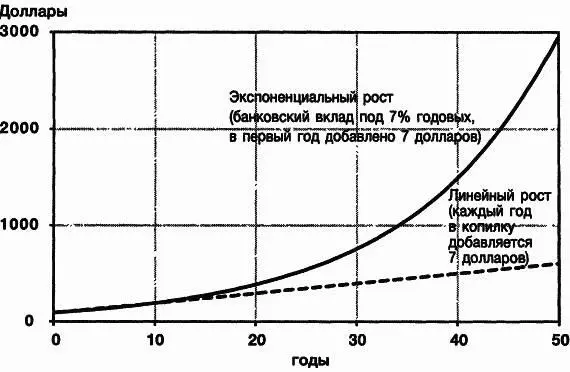
Рис. 2.3. Сравнение линейного и экспоненциального роста накоплений Если положить 100 долларов в копилку и каждый год добавлять по 7 долларов, накопления растут линейно, как показано пунктирной линией. Если положить 100 долларов в банк под 7 % годовых, сумма будет расти экспоненциально, со временем удвоения примерно 10 лет.

на большую величину. Процент фиксирован — он по-прежнему составляет 7 % в год, но в абсолютном выражении — в долларах — приращение будет увеличиваться ежегодно. В первый год приращение составит 7 долларов. Во второй год 7 % будут рассчитываться уже от 107 долларов, приращение составит 7,49 долларов, и сумма вклада увеличится до 114,49. Годом позже приращение будет уже 8,01 долларов, а сумма вклада 122,50. К концу десятого года на счете будет 196,72 доллара.

Если же вы положите 100 долларов в копилку и каждый год будете добавлять к ее содержимому по 7 долларов, сумма будет расти линейно. В конце первого года в копилке будет 107 долларов, точно так же, как и на счете в банке. Но в конце десятого года в копилке будет 170 долларов, то есть меньше, чем в банке, хотя разница не настолько велика, чтобы огорчаться.

Поначалу оба вида роста ведут себя похожим образом, но в один прекрасный момент взрывной характер экспоненциального роста себя проявит (рис. 2.3). Через 20 лет в копилке будет 240 долларов, тогда как на банковском счете почти 400 долларов. К концу тридцатого года линейный рост в копилке даст всего 310 долларов, а банковский вклад под 7 % годовых будет располагать суммой в 761 доллар. За 30 лет экспоненциальный рост под 7 % годовых обеспечил разницу в сравнении с линейным ростом больше чем вдвое, хотя стартовая сумма была одинаковая.

В конце пятидесятого года сумма в банке будет в 6,5 раза больше, чем в копилке — разница составит почти 2500 долларов.

Удивительные результаты экспоненциального роста на протяжении столетий приводили людей в восхищение. Существует старая персидская легенда об одном мудром придворном, который подарил своему повелителю прекрасно отделанную шахматную доску, а взамен попросил дать ему 1 зернышко риса за первую клетку, 2 зернышка за вторую, 4 за третью и т. д.

Повелитель согласился и приказал нести рис из кладовых. Для четвертой клетки шахматной доски потребовалось 8 зерен, для десятой — 512, для пятнадцатой — 16 384, а для двадцать первой — уже больше миллиона. К сорок первой клетке число зерен превысило триллион (10 12). Чтобы расплатиться за все 64 клетки доски, не хватило бы всех запасов риса в мире.

Детская французская загадка иллюстрирует другую характерную черту экспоненциального роста — внезапность, с которой экспоненциально растущая величина достигает определенного предела. Предположим, у вас есть пруд, в котором растет одна кувшинка. Каждый день число кувшинок удваивается. Если позволить им расти бесконтрольно, за 30 дней они покроют всю поверхность пруда, уничтожив в нем все другие формы жизни. Но поначалу кажется, что кувшинок не так уж и много, так что они не вызывают у вас беспокойства, по крайней мере пока не заполонят половину пруда. На какой день это произойдет и сколько времени у вас будет, чтобы спасти пруд?

На спасение пруда у вас будет всего один день, потому что кувшинки покроют половину поверхности на 29-й день. На следующий день, после финального удвоения, пруд будет покрыт ими полностью. Это только поначалу кажется разумным отложить принятие мер до того момента, когда пруд будет закрыт кувшинками наполовину. На 21-й день растения покрывают примерно 0,2 % поверхности. На 25-й день закрыто 3 % зеркала воды. И все равно при таком подходе на спасение пруда у вас будет всего один день [17].

Из этого примера видно, каким образом экспоненциальный рост в сочетании с запаздыванием реакции может привести к выходу за пределы. Поначалу долгое время рост кажется незначительным, никто и не думает, что это может вызвать какие-то проблемы. Но затем он становится все быстрее и быстрее, пока за последние одно-два удвоения время на реагирование не истечет. В развитии событий в пруду с кувшинками за последний день не происходит никаких принципиальных изменений, процент роста был постоянным весь месяц, от начала и до конца. Просто получается, что в определенный момент экспоненциальный рост набирает такую силу, что справиться с ним уже невозможно.

Особенности экспоненциального роста, его переход от незначительных величин к выходу за пределы можно попробовать на себе. Представьте себе, что вам надо съесть один орешек в первый день месяца, два — во второй день, четыре — в третий и т. д. Сначала вы покупаете и едите орехи по чуть-чуть. Но задолго до конца месяца у вас уже будут проблемы с желудком и состоянием банковского счета. Сколько вы сумеете продержаться, соблюдая экспоненциальную зависимость? На десятый день вам надо будет съесть примерно полкило орехов. А на тридцатый день месяца, чтобы соблюсти принцип удвоения, вам придется купить и съесть больше 500 т!