Петр Путенихин - Двигатель космолёта на эффекте гравитационного самоускорения

На рисунке, как видим, вследствие этого возник такой пилообразный контур потенциала. Если сделать скачки бесконечно малыми, что ширина «зубьев» пилы уменьшится до нуля, и контур её станет плавной кривой. Хорошо заметно, что этот контур в пространстве оказывается смещённым по отношению к графику гравитационного потенциала. В реальности это будет выглядеть так, будто гравитационный потенциал Солнца как бы «вытянут» в пространстве, он явно «отстаёт» от своего источника – Солнца:

Рис.3 При плавном движении Солнца его гравитационный потенциал «вытягивается» в пространстве, отстаёт от своего источника.

Вблизи от удаляющегося Солнца потенциал снижается практически мгновенно, поскольку столь короткое расстояние фронт проходит очень быстро. Чем дальше точка от Солнца, тем позднее в неё придёт фронт изменившегося потенциала. Кроме того на момент его прихода Солнце уже переместится в новую точку, что и выглядит как «вытягивание» потенциала. Чем точка дальше, тем сильнее в ней потенциал отстаёт от уровня, соответствующего неподвижному Солнцу: по горизонтали точки равного потенциала отстоят на всё большем расстоянии при удалении от него. Это отставание также возрастает с увеличением скорости движения гравитирующего тела, как показано на предыдущем рисунке, напоминающем детский самокат без заднего колеса. На начальном этапе движения скорость велика и отставание гравитационного потенциала движущегося тела от потенциала покоящегося также велико. По мере снижения скорости движения тела отставание уменьшается и становится равным нулю при остановке тела.

Безопорное движение

Такое «вытягивание» потенциала, зависящего от скорости удаления Солнца, наводит на интересную мысль. А что, если «получатель потенциала», скажем, измерительный прибор не покоится, а тоже движется со скоростью Солнца? При неподвижных Солнце и приборе всё ясно: потенциал всегда один и тот же. Но при движении Солнца потенциал не просто движется за ним, а немного отстаёт, что приводит к его своеобразному «вытягиванию», «растяжению», запаздыванию. Если измерительный прибор находится на фиксированном расстоянии от Солнца, двигаясь с точно такой же скоростью, что и оно, то он, тем не менее, должен зафиксировать изменение потенциала. Причём очевидно, что прибор будет фиксировать увеличение этого потенциала.

Поскольку скорость объектов одна и та же, им можно назначить одну и ту же систему отсчета и даже связать их неким условным стержнем. Поскольку стержнем соединиться с Солнцем нельзя, рассмотрим другой объект. Пусть два точечных тела равной массы m соединены твёрдым невесомым стержнем длиной r. Если эта система изначально находится в прямолинейном равномерном движении вдоль своей оси, то, как мы обнаружили в примере с Солнцем, на заднюю массу будет действовать дополнительная сила притяжения от головной точки по сравнению с состоянием покоя. А это непосредственно означает, что эта сила не будет уравновешена силой упругого сжатия стержня и приведёт эту массу в ускоренное движение.

Но, можно возразить, такая же сила, вероятно, действует и на головную массу, тормозя систему? Нет! Для головной массы действует эффект в точности противоположный. Гравитационный потенциал ведомой массы отстаёт от ведущей, поэтому ведущая масса оказывается под воздействием уменьшенной силы от притяжения ведомой. Поэтому она так же не будет уравновешена силой сжатия стержня, и стержень будет толкать эту массу вперёд.

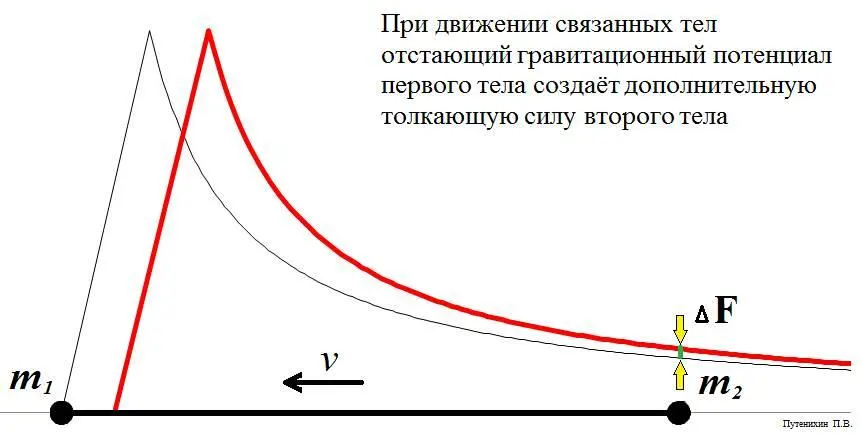
Рис.4. Массы на концах движущегося стрежня испытывают неуравновешенную силу, превышающую силу их гравитационного притяжения в состоянии покоя.

Выходит, что стержень под воздействием этих неожиданных сил начнёт ускоряться. Причём, из состояния покоя стержень сам в движение не придёт, ему необходимо дать некоторую начальную скорость вдоль его оси.

Конечно, можно возразить: дополнительная сила притяжения просто сожмёт стержень, и он станет короче. Но этого не может произойти. Деформация отстающего конца стержня постепенно (не быстрее скорости света) передастся на его передний край, конец стержня будет стремиться переместиться вперёд. Этому будет препятствовать ведущая масса. За счёт чего? Сила притяжения этой массы от отстающего тела всегда меньше той, что соответствует исходной, «несжатой» длине стержня, поскольку для ведущей массы расстояние до ведомой «кажется» более длинным. Поэтому в ведущей, передней по движению массы не появится дополнительной силы, чтобы компенсировать возросшую силу давления от связующего стержня.

Давайте оценим величину этих сил и возникшего от их действия ускорения. В состоянии покоя массы притягиваются с силой согласно закону Ньютона:

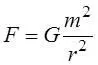
где

F – сила притяжения точечных масс;

m – массы на концах стержня;

r – длина стержня;

G – гравитационная постоянная.

Путь стержень движется со скоростью v вдоль своей оси. За некоторый момент времени ведущая масса переместится из точки a в точку a' , а ведомая – из точки b в точку b' . Из точки a' гравитационный потенциал ведущей массы начал создавать обновленные значения поля в направлении ведомой массы со скоростью света – с . До того момента, когда фронт прибудет в точку b' , там «действует» прежнее, большее значение потенциала.

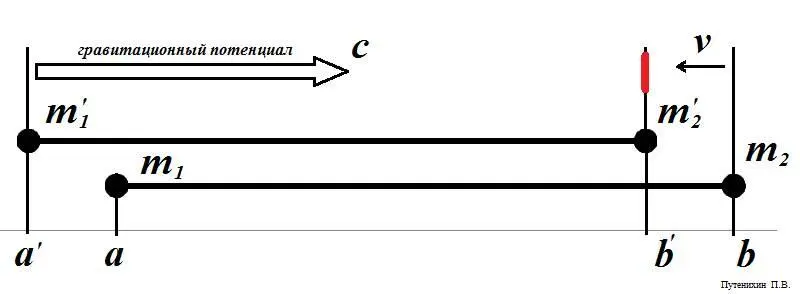
Рис.5. Масса в конце движущегося стрежня испытывают силу, как если бы длина стержня была меньше исходной

Ведомая масса движется навстречу этому фронту со скоростью v , находясь в поле с последним значением потенциала. Поскольку на начало движения расстояние между массами было равно r , фронт от ведущей массы встретится с ведомой массой в точке, отмеченной красной чертой, через время t = r / (c + v) . За это время ведомая масса приблизится к точке, из которой началось движение фронта нового значения потенциала, на расстояние b – b' = r1 = vt = rv / (c + v) . Следовательно, ведомая масса окажется в точке с потенциалом, соответствующим этому изменённому расстоянию

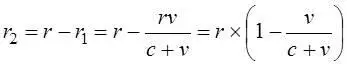
В дальнейших расчетах будем скорость движения стержня измерять в долях от скорости света v = kc , назвав для наглядности эту безразмерную величину k той же буквой v , что и размерную скорость стержня: