Анна Смирнова - О чем рассказали «говорящие» обезьяны: Способны ли высшие животные оперировать символами?

Птицы с первых же проб решали эту задачу правильно: в достоверном большинстве случаев они выбирали цифру, соответствующую изображенному на образце множеству и наоборот. Следовательно, вороны способны без специального обучения, за счет мысленного сопоставления ранее полученной информации, установить эквивалентность множеств и исходно индифферентных для них знаков (цифр от 1 до 4).

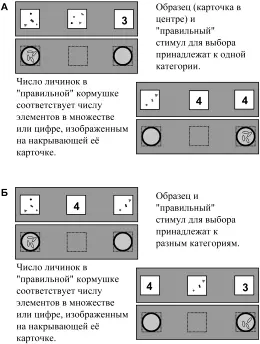
Мы предполагаем, что в данном случае птица принимала решение с помощью операции логического вывода, которую называют транзитивным заключением (см. ниже, раздел «Операции логического вывода»). Поскольку ранее каждому графическому множеству и каждой цифре соответствовало определенное число личинок, то выбирать нужно тот стимул, за который ранее давали столько же личинок, сколько и за образец (если А = В и В = С, то А = С). То есть, на основе двух посылок, полученных ассоциативным или условно-рефлекторным путем, животное может сделать вывод о наличии третьей связи.

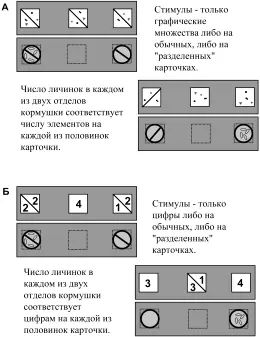
В следующем эксперименте мы выясняли, могут ли птицы оперировать усвоенной информацией – выполнять с цифрами комбинаторную операцию, аналогичную арифметическому сложению. «Слагаемые» (цифры или множества) были изображены на карточках, разделенных по диагонали чертой, так же как и соответствующие им кормушки были разделены вертикальной перегородкой на две равные части (рис. 10А). В «демонстрационной» серии использовали только множества либо на обычных, либо на «разделенных» карточках и демонстрировали соответствие числа элементов на обычных либо на «разделенных» карточках числу личинок в обычных или в «разделенных» кормушках.

В отличие от «демонстрационной» серии, в тесте на «сложение» мы использовали только цифры. Если в качестве образца предъявляли отдельную цифру, то для выбора – две «разделенные» карточки с цифрой в каждой половине, сумма которых на одной из них соответствовала цифре на образце (рис. 10Б). Если в качестве образца использовали «разделенную» карточку с парой цифр, то для выбора предлагали отдельные цифры.

Птицы успешно справились с этой задачей. К началу серии они уже знали, что каждому конкретному графическому множеству и каждой цифре соответствует определенное число личинок, и на этом основании во время теста они (экстренно) определяли, что определенные цифры и графические множества соответствуют друг другу. Затем, в ходе демонстрационной серии вороны получали дополнительную информацию о том, что под карточкой с «разделенным» множеством находится соответствующим образом «разделенное» число личинок. Для правильного выполнения теста на «сложение» им нужно было сделать мысленное заключение об эквивалентности друг другу отдельных цифр и соответствующих комбинаций двух цифр.

Оказалось, что вороны способны сохранять информацию о числовых признаках стимулов не только в форме образных представлений, но и в некой отвлеченной и обобщенной форме, которую они смогли связать с ранее нейтральными для них знаками – цифрами. Следовательно, не только у высших приматов, но и у некоторых птиц довербальное мышление достигло в своем развитии того промежуточного этапа, который, по мнению Орбели (1949), обеспечивает возможность использования символов вместо реальных объектов и явлений и который в эволюции предшествовал формированию второй сигнальной системы.

Основываясь на результатах целого ряда поведенческих тестов, Л. В. Крушинский (1986) высказал предположение о существовании параллелизма в эволюции высших когнитивных функций птиц и млекопитающих – позвоночных с разными типами структурно-функциональной организации мозга. Мы привели эти данные, чтобы показать, что обобщение, абстрагирование, формирование довербальных понятий и способность к символизации – достаточно универсальные когнитивные операции, в сходной степени присущие высшим представителям разных классов позвоночных.

С тех пор всё новые и новые данные подтверждают, что, несмотря на принадлежность к различным ветвям эволюции и кардинальные различия в структуре мозга, способность к разным видам элементарного мышления, в том числе к обобщению и абстрагированию, у представителей этих классов характеризуется сходными градациями. Это свидетельствует о том, что предыстория человеческого мышления восходит к достаточно древним этапам филогенеза, общим для предков этих классов.

Говоря о мышлении животных в контексте обучения обезьян языкам-посредникам, нельзя не упомянуть о способности животных к совершению двух операций логического вывода (inferential reasoning), когда при получении новой информации ее усвоение происходит на основе уже имеющейся, путем мысленного сопоставления ранее полученных сведений. Об этих операциях необходимо упомянуть по двум причинам. Во-первых, само начало их изучения связано с именем Д. Примэка – одного из первопроходцев в области изучения зачатков речи у обезьян (Gillan et al. 1981; Premack 1983; Premack & Premack 1972, 2003). Во-вторых, одна из операций – транзитивное заключение – тесно связана с процессом символизации.

Упомянутое выше транзитивное заключение составляет одну из базовых операций, присущих дедуктивному мышлению человека. Определение транзитивного отношения пришло в психологию из формальной и математической логики. Отношение r называют транзитивным, если оно, попарно связывая стимулы B и C, C и D, с необходимостью связывает также стимулы B и D. Стимулы, связанные такими отношениями, образуют транзитивный ряд: B r C r D. Таким образом, если субъект способен из двух предпосылок B r C и C r D сделать вывод, что B r D, то говорят, что он способен к транзитивному заключению. Примерами транзитивных отношений могут служить такие, как «больше, чем» (например, если B > C и C > D, то B > D), «дальше», «ярче» и т. д. Наряду с отношением транзитивных неравенств существует и возможность транзитивного равенства: если A=B и B=C, то A=С. Именно эта операция, как мы увидим, вовлечена в процесс символизации у птиц – в превращение нейтральных для них стимулов (цифр) в символы-числительные, которыми они далее оперируют вместо соответствующих множеств.