Юрий Степанов - Концепты. Тонкая пленка цивилизации

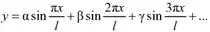
(l – длина струны, а = a(t), β = β(t), γ = γ(t)…) – (по работе: К. А. Рыбников. История математики. М., 1974. С. 207).

Более точным математическим анализом может служить понятие «гармонического ряда». Название связано с тем, что струна при делении ее на 2, 3, 4, равные части дает звуки, гармонирующие с основным тоном («Справочник по высшей математике» [Выгодский 1995: 536]).

(Культурологу здесь может быть необходимо, как нам думается, целое математическое п р и м е ч а н и е, для которого просто указываем соответствующую страницу названной книги М. Я. Выгодского (с. 532–533).)

Мы продолжаем историческое изложение К. А. Рыбникова. «Однако Эйлер выступил против такой трактовки общего решения, так как, по его мнению, функция, предложенная Д. Бернулли, являлась недостаточно общей. В самом деле, она непрерывная, нечетная, периодическая. Поэтому, по Эйлеру, она могла выражать лишь частное решение, в крайнем случае – класс частных решений. Возникший спор привел к задаче: выяснить объем класса функций, представи—мых тригонометрическими рядами.

В 1807 г. (опубликовано в 1822) Фурье в работах по аналитической теории тепла показал, что [.] все эйлеровские связанные кривые, начерченные свободным движением руки, оказались охваченными аналитическим аппаратом тригонометрических рядов» [Рыбников 1974: 207].

Мы продолжаем изложение К. А. Рыбникова (с. 209, 354). В 1822 г. Фурье опубликовал «аналитическую теорию тепла», оказавшую огромное влияние на развитие математики, в дальнейшем математические методы, ведущие свое начало от Фурье, в соединении с соображениями о законах сохранения энергии (С. Карно, 1824; Р. Майер; Г. Гельмгольц; Дж. Джоуль – 1840–е; Р. Клаузиус, 1850; У. Томсон—Кельвин, 1851) привели к формулировке второго начала термодинамики и установлению понятия энтропии.

Однако сейчас для развития нашей темы нам важны не столько общие принципы вроде начал термодинамики, энтропии и т. п., сколько более конкретные исследовательские понятия, в частности, понятие функции. Это понятие очень популярно у современных исследователей разных областей науки. Математик и культуролог А. Н. П а р ш и н исследовал «числа как функции» [Паршин 2002: 7 и сл. ] (культурологам, в частности, будет интересно «рисунчатое, движением руки, изображение» кривой и знака функции).

Необходимые К. А. Рыбникову для его «Истории математики» (с. 354) ссылки на Л. Больцмана и, самое главное, на развитие понятия функции (с. 200, 206 и сл.) оказываются параллельными (как «изотемы») ссылкам автора данной книги для его истории культуры (например, в работе «Язык и метод. К современной философии языка» [Степанов 1998: 332, 495]; в работе «Функции и глубинное» [Степанов 2002] и др.). По этой причине последнюю изотему мы подчеркнем отдельно – в следующем разделе.

Логико—математическое понятие функции является в настоящее время, несомненно, центральным по положению в нашей системе рассуждения и содержательно важнейшим для нашей цели. Им вводится целый класс математико—лингвистических аналогий, параллелей и исследовательских ситуаций. Ниже нумеруем их – в порядке возникновения в нашем рассуждении – цифрами от 1 и далее; но эта нумерация все же связана до некоторой степени с иерархией понятий в системе.

Теперь рассмотрим более конкретно группу лингвистических явлений, составляющих параллели, аналоги, аналогии (все эти термины для нас равнозначны) к логико—математическим понятиям, покрываемым общим понятием «Функция» или находящимся в какой—либо существенной связи с ним. Для этого «слева» указываем то или иное необходимое частное понятие функции в математическом смысле или контексте, а «справа» его лингвистический аналог.

Таким образом, нижеследующий текст представляет собой своего рода двуязычный словарь, хотя в типографском отношении входной «левый» термин и «переводной» «правый» могут быть разъединены несколькими строками или даже абзацами.

Лейтмотивом в классе «Функция» является для нас (для лингвиста) идея процесса (вычисления или построения), но, как мы увидим уже в разделе 1, со стороны математики именно ее важность иногда отрицается.

1. Рекурсивные функции и предикаты: процесс и рекурсия.Дж. Литлвуд, рассматривая (резко критически) книгу А. Р. Форсайта «Теория функций комплексного переменного», изданную в 1893 г., но все еще читаемую, цитирует из нее: «Возникновение идеи функциональности вначале было связано с функциями вещественных переменных, и тогда эта идея была равнозначна идее зависимости. Так, если X зависит от значения x и не зависит ни от какой другой изменяющейся величины, то принято X рассматривать как функцию от х; при этом обычно еще

подразумевается, что X выводится из х при помощи ряда операций». Такое изложение, по мнению Литлвуда, навевает «общий кошмар». «В наше время, – продолжает он, – конечно, функция у = у(х) означает, что имеется класс «аргументов» х и что каждому х поставлено в соответствие 1 и только 1 «значение» у. После некоторых тривиальных разъяснений (а может быть, и без них?) мы можем осмелиться сказать, что функция есть просто класс С пар (х, у) (с учетом порядка в скобках), подчиненный (только) тому условию, что х в различных парах должны быть различными (и утверждение «между х и у есть зависимость R» означает просто задание класса, который может быть любым классом упорядоченных пар)» [Литлвуд 1978: 64, 67].

Если термины «изменяющаяся величина», «выводится», «ряд операций» и т. п. вызывают у Дж. Литлвуда «ощущение кошмара», то он упускает и связанную с ними более общую идею «процесса», хотя бы понятия вычислимости. А эта идея и является в настоящее время самой главной.

Изложенное определение в курсах математической логики описывает класс функций, называемых примитивно—рекурсивными функциями: «функция f (t,x), содержащая или не содержащая параметр t, называется примитивно—рекурсивной относительно функций a(t), b(t, x, y), если

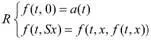
(где никакая переменная, встречающаяся в правой части уравнения, не отсутствует в левой части, хотя некоторые переменные и могут отсутствовать в правой части)» [Гудстейн 1961: 73].

Р. Л. Гудстейн обращает внимание на черту аналогии с языком: «Предложение, содержащее свободные переменные, есть арифметический предикат» [Гудстейн 1961: 68].