Array Коллектив авторов - Инновационные и приоритетные направления в преподавании гуманитарных дисциплин в техническом вузе. Сборник трудов по материалам III Международной научно-практической конференции 21 апреля 2016 г.

Пример.В ящике находятся детали первого, второго и третьего сорта. Наудачу извлекается одна деталь. Событие А – деталь первого сорта. Событие В – деталь второго сорта. Событие С – деталь третьего сорта. Сформулируйте, что представляет собой событие: А+В,, АС, АВ+С.

Решение.Событие: А+В означает, что вынута деталь первого или второго сорта.

Событие:, то есть вынута деталь второго сорта, так как событие А+С означает, что деталь первого или третьего сорта. Событие: АС – невозможное, так как деталь не может быть одновременно и первого и третьего сорта. Событие: АВ+С – это сумма невозможного АВ и С, то есть деталь третьего сорта.

Таким образом, развитие математической речи в курсе теории вероятностей – это очередной этап учебно-исследовательской деятельности по формированию у студентов математически верной устной и письменной речи. В математическом языке выделяет два компонента: язык данной математической теории (каждый раздел математики пользуется своим особым языком) и логический язык, состоящий из терминов и символов, обозначающих логические операции, используемые для конструирования предложений и для вывода одних предложений из других [2].

Формированию культуры математической речи может способствовать специально разработанная система задач, в которую целесообразно включать следующие задания [2]:

Задания для работы с терминологией, символикой и графическими изображениями.

Задания для работы со словесно-логическими конструкциями математического языка.

Задания для работы с письменными обучающими текстами по математике.

Виды математической речи можно представить в виде следующей таблицы, где для каждого вида сформулированы конкретные приемы для их развития (рис.1).

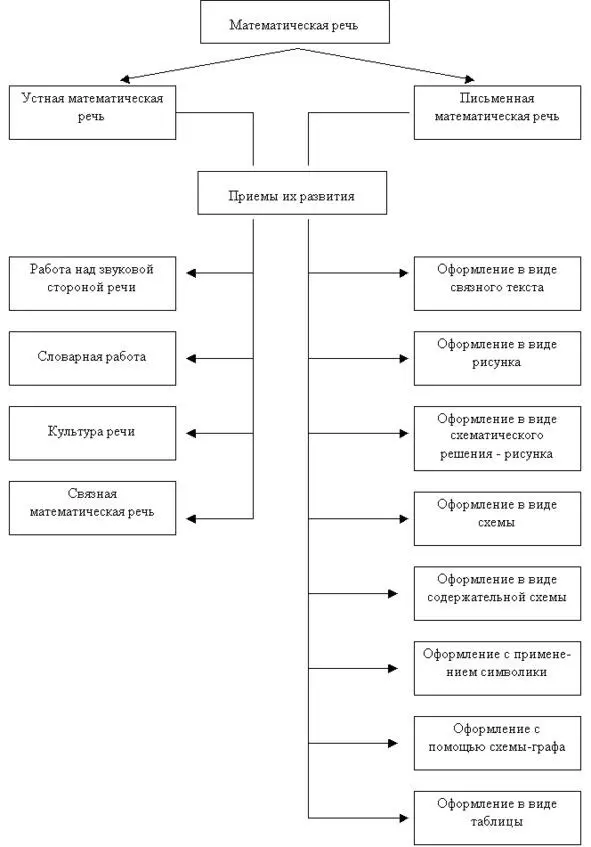
Рисунок 1

Рассмотрим простейшие примеры приемов развития устной математической речи.

Работа над звуковой стороной речиозначает формирование правильного произношения и выразительного чтения математических терминов и любого задания. Для успешного решения этой задачи студентам надо следить, прежде всего, за речью преподавателя.

Словарная работана занятиях математики сводится к пониманию и умению объяснять значение математических терминов, усвоению их правильного написания и формированию умений составлять содержательное связное высказывание. С этой целью полезно выполнить упражнения следующих видов:

1) упражнения на объяснение значений математических терминов (объясните значение слов и выражений: функция, аргумент, дифференциал, экспонента);

2) упражнения на составление правильных связных высказываний (прочитайте предложения, вставив пропущенные слова: « С геометрической точки зрения производная …, вычисленная… равна… касательной, проведенной к… функции в точке, с…» .

Формирование культуры математической речиприводит к устранению грамматических и математических ошибок и речевых недостатков таких как, неточность и бедность речи, употребление лишних слов, неправильный порядок слов в предложении. На этом этапе работы по развитию речи достигается ясность и точность речи.

Развитие связной математической речипроисходит в соответствии с требованиями к развитию речи, таких же, как и на занятиях по гуманитарным дисциплинам или на уроках литературы. Для решения этой задачи важную роль играет такой раздел учебно-методического комплекса по дисциплине как глоссарий. Включение этого раздела в каждый разрабатываемый преподавателем УМК и активное его использование в процессе аудиторных занятий и в различных формах промежуточного и итогового контроля положительно скажется на улучшении качества речи студентов.

Приемы развития письменной речи лучше показать на примерах оформления решения задач. При этом следует помнить: нужно не только учиться правильно мыслить, но и правильно говорить, писать коротко и ясно.

1. Оформление решения в виде связного текста.

Пример (на формулу полной вероятности).Некоторая фирма собирается заключить контракт на поставку своей продукции. Вероятность получения контракта оценивается в 0,45; в противном случае – в 0,25. По оценкам экспертов компании вероятность того, что конкурент выдвинет свои предложения по заключению контракта, равна 0,40. Чему равна вероятность заключения контракта для этой фирмы?

Решение.Пусть событие А = «фирма заключит контракт»; гипотеза H 1 = «конкурент выдвинет свои предложения»; гипотеза H 2 = «конкурент не выдвинет свои предложения». По условию задачи: P (H 1) = 0.4, P (H 2) = 1—0.4 = 0.6. Вычислим условные вероятности по заключению контракта для фирмы: P (A/H 1) = 0.25, P (A/H 2) = 0.45. По формуле полной вероятности получаем: P (A) = 0.4•0.25+0.6•0.45 = 0.37.

2. Оформление в виде рисунка (графика).

Пример.Является ли функцией распределения некоторой случайной величины следующая функция

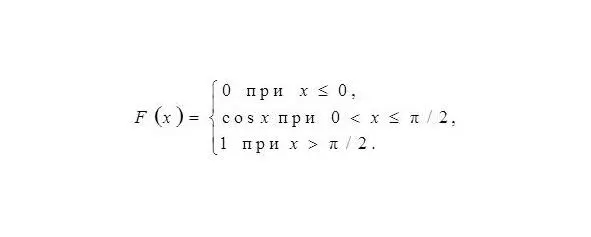
Решение.Данная функция не может являться функцией распределения некоторой случайной величины, так как на промежутке (0; π/2] она убывает и не является непрерывной. График функции изображен на рис. 2.

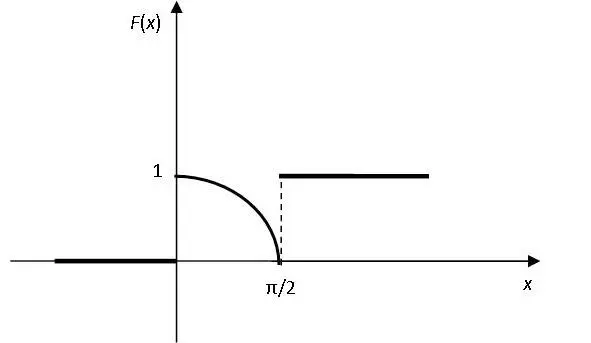
Рисунок 2

3. Оформление в виде схематического решения – рисунка.

Решение.Смотри рис.3.

Пример.Исследовать линии уровня функции z=x 2+y 2и изобразить их.

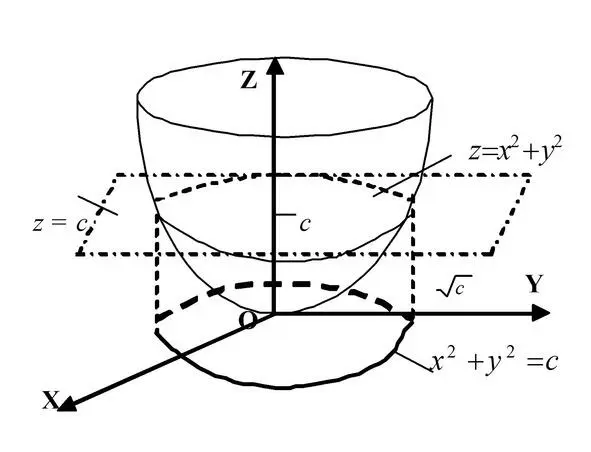
Рисунок 3

Решение оформлено в виде схематического решения – рисунка.

4. Оформление в виде схемы (блок-схемы) и создание мультимедийной презентации

Пример.Составить блок-схему по теме интегрирование рациональных функций.

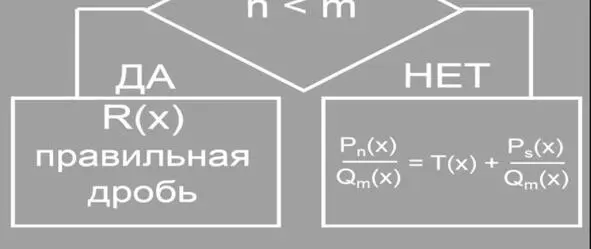
Рисунок 4

Решение оформлено в виде блок-схемы (рис.4).

4. Оформление в виде содержательной схемы.

Пример.Туристу необходимо прибыть в некоторый населенный пункт, находящийся на расстоянии 134,7 км от его дома. 2,4 часа он ехал на автобусе со скоростью 55 км/ч, а остальную часть пути он шел пешком со скоростью 4,5 км/ч. Сколько времени он шел пешком?

Решение этой задачи оформлено в виде содержательной схемы (рис.5).