Александр Акилов - Голография для любознательных. Книга для научных сотрудников школьного возраста

– Каждый цвет уже присутствует в белом свете. Все цвета передаются через межпланетное пространство и атмосферу совместно и дают эффект в виде белого света. Белый свет – смесь разнообразных корпускул.

Корпускулярная теория Ньютона удовлетворительно объяснила многие оптические явления, известные в то время. Ее автор пользовался в научном мире колоссальным авторитетом, и вскоре теория Ньютона приобрела многих сторонников во всех странах. Но, как часто бывает, даже великий Ньютон в своих опытах кое—что не разглядел.

Томас Юнг (13.06.1773 – 10.05.1829)

Эксперимент, проведенный Томасом Юнгом в начале XIX века, стал неоспоримым доказательством волновой природы света. Он рассмотрел весьма скрупулезно явления, связанные с прохождением света сквозь малые отверстия. Результаты одного из экспериментов были опубликованы автором в 1803 году.

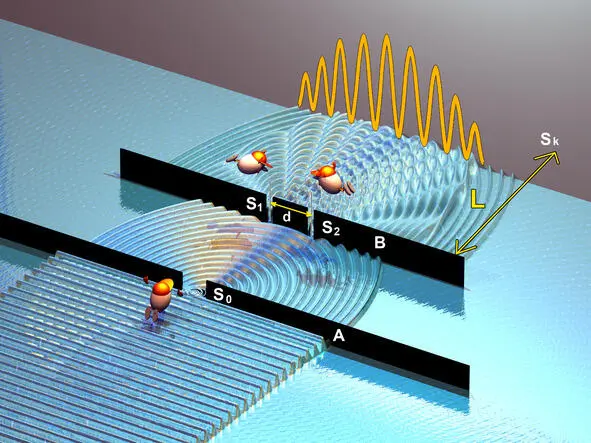
Свет от удаленного источника S проходил через узкую щель S 0в экране А, затем попадал на экран В с двумя щелями S 1и S 2, расположенными достаточно близко друг к другу на расстоянии d. Экран S располагался на расстоянии L от щелей, причем L>> d

В опыте Юнга использовался необычный пучок света, который он получал разделением и последующим сведением световых лучей, исходящих из одного и того же источника. Рассмотрим схему эксперимента Юнга. Свет от удаленного источника (S) проходил через узкую щель (S 0) в экране (А), затем попадал на экран (В) с двумя щелями (S 1) и (S 2), расположенными достаточно близко друг к другу на расстоянии (d). Экран (Sk) располагался на расстоянии (L) от щелей, причем L>> d. Если бы свет представлял собой поток частиц, то на экране (S k) можно было увидеть только два световых пятна на расстоянии (L) от экрана (В). Однако Юнг увидел периодическую картину светлых и темных полос. Самая яркая полоса располагалась на оси оптической схемы как раз посередине, между щелями (S 1) и (S 2). На основании увиденного, Юнг сделал вывод, что свет представляет собой волну, а не поток частиц, как до этого эксперимента со всей авторитетностью утверждал гениальный Исаак Ньютон.

Огюстен Френель (10.05.1788 – 14.07.1827)

Молодого дорожного инженера Огюстена Френеля, присоединившегося волонтером к роялистским войскам, которые должны были преградить дорогу Наполеону во время его возвращения с острова Эльба, уволили со службы, и он вынужден был уехать домой и посвятить свободное время исследованию дифракции, имея в своем распоряжении лишь случайное и примитивное экспериментальное оборудование. Два доклада, представленных им 15 октября 1815 года Парижской Академии наук, были первым результатом этих трудов. Френель был приглашен в Париж для повторения своих опытов в более благоприятных условиях. Френель начал исследовать тени, отбрасываемые небольшими препятствиями на пути лучей, и обнаружил образование полос не только снаружи, но и внутри тени, что до него уже наблюдал ученый Гримальди (1618—1663) и о чем лукаво умолчал Ньютон. Исследование тени, образуемой тонкой проволокой, привело Френеля к повторному открытию принципа интерференции после Томаса Юнга. «Внутренние каемки не могут образовываться от простого смешения этих лучей, потому что каждая сторона проволоки в отдельности направляет тень только на непрерывный поток света; следовательно, каемки образуются в результате перекрещивания этих лучей», – писал в своем докладе молодой ученый. Этот вывод, который представляет собой, так сказать, перевод явления на понятный язык, полностью противоречит гипотезе Ньютона и подтверждает теорию световых колебаний. Легко можно догадаться, что колебания двух лучей, которые скрещиваются под очень малым углом, могут взаимодействовать, образуя картину интерференции.

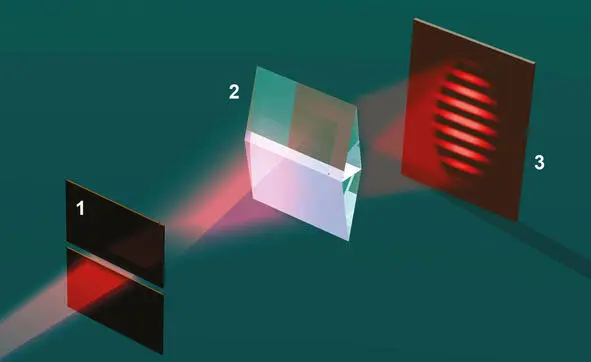
Свет направляется на симметричную бипризму (2) от яркого источника через узкую щель (1), которая собирает два пучка света на экране (3). В результате сложения этих пучков возникает периодическая картина интерференции

В Париже Френель узнал об опытах Юнга с двумя отверстиями, которые, по его мнению, были вполне подходящими для иллюстрации волновой природы света. Для исключения всякой возможности истолкования этого явления, как действия краев отверстий, Френель придумал известный «опыт с двумя зеркалами», о котором он сообщает в 1816г., а затем в 1819 году «опыт с бипризмой», ставший с тех пор классическим методом демонстрации принципа интерференции. Свет направляется на симметричную бипризму (2) от яркого источника через узкую щель (1), которая собирает два пучка света на экране (3). В результате сложения этих пучков возникает периодическая картина интерференции. Взяв на вооружение явление интерференции, Френель располагал теперь тремя принципами: принципом элементарных волн, принципом огибающей и принципом интерференции. Это были три отдельных принципа, которые Френель гениально решил слить воедино. Таким образом, для Френеля «огибающая» волн в явлении преломления света не просто геометрическое понятие, как для Гюйгенса, а представляет собой алгебраическую сумму импульсов, создаваемых каждой элементарной волной. Полная сумма всех этих импульсов складывается согласно принципу интерференции и в частном случае может быть равна нулю. Другими словами, световые волны одинаковой длины могут складываться и вычитаться в зависимости от значения их фаз в некоторой точке пространства.

Благодаря опытам Юнга и Френеля, монохроматическую плоскую световую волну в общем случае можно описать функцией вида:

ξ (x,t) = A*cos (ωt – kx + φ 0), где:

ξ (x,t) – смещение частицы среды, находящейся на расстоянии (х) от источника колебаний в момент времени (t);

A – амплитуда колебаний;

ω – круговая (циклическая) частота, ω= kν;

ν = 1/Т – частота электромагнитных колебаний;

k – волновое число, k=2π/λ;

λ – длина волны;

υ – скорость распространения волны, υ = λ/T;

Т – период колебаний;

φ 0 – начальная фаза колебаний.

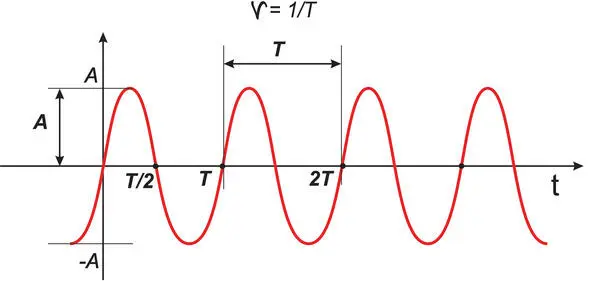
График зависимости смещения волны от времени