Гидравлика
- Название:Гидравлика
- Автор:
- Жанр:
- Издательство:Array Литагент «Научная книга»
- Год:2008
- Город:Москва
- ISBN:978-5-699-24848-3
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Гидравлика краткое содержание
Гидравлика - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Поэтому выражение для центра давления (точка D) без переноса оси момента инерции от той же линии уреза, совпадающие с осью O Y, будет иметь вид:
I y= I 0+ ωl 2 ц.т.
Окончательная формула для определения места расположения центра давления от оси уреза жидкости:
l ц. д.= l ц. г.+ I 0/S.
где S = ωl ц.д.– статистический момент.
Окончательная формула для l ц.д.позволяет определить центр давления при расчетах гидротехнических сооружений: для этого разбивают участок на составные участки, находят для каждого участка l ц.д.относительно линии пересечения этого участка (можно пользоваться продолжением этой линии) со свободной поверхностью.
Центры давления каждого из участков находятся ниже центра тяжести смоченной площади по наклонной стенке, точнее по оси симметрии, на расстоянии I 0/ωl ц.u.
11. Общая методика определения сил на криволинейные поверхности
1. В общем случае, это давление:
P z= ρgWg,
где Wg – обьем рассматриваемой призмы.
В частном случае, направления линий действия силы на криволинейную поверхность тела, давления зависят от направляющих косинусов следующего вида:
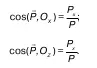
Сила давления на цилиндрическую поверхность с горизонтальной образующей полностью определена. В рассматриваемом случае ось O Yнаправлена параллельно горизонтальной образующей.
2. Теперь рассмотрим цилиндрическую поверхность с вертикальной образующей и направим ось O Zпараллельно этой образующей, что значит ω z= 0.
Поэтому по аналогии, как и в предыдущем случае,
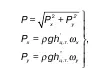
где h' ц.т.– глубина центра тяжести проекции под пьезометрическую плоскость;
h' ц.т.– то же самое, только для ω y.
Аналогично, направление определяется направляющими косинусами
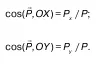
Если рассмотреть цилиндрическую поверхность, точнее, объемный сектор, с радиусом γ и высотой h, с вертикальной образующей, то
ω x= h y,
h' ц.т.= 0,5h.
3. Осталось обобщить полученные формулы для прикладного применения произвольной криволинейной поверхности:
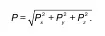
12. Закон Архимеда. Условия плавучести погруженных тел
Следует выяснить условия равновесия погруженного в жидкость тела и следствия, вытекающие из этих условий.
Сила, действующая на погруженное тело – равнодействующая вертикальных составляющих P z1, P z2,т. е.:
P z1= P z1– P z2= ρgW Т. (1)
где P z1, P z2– силы направленные вниз и вверх.
Это выражение характеризует силу, которую принято называть архимедовой силой.
Архимедовой силой является сила, равная весу погруженного тела (или его части): эта сила приложена в центр тяжести, направлена вверх и количественно равна весу жидкости, вытесненной погруженным телом или его частью. Мы сформулировали закон Архимеда.
Теперь разберемся с основными условиями плавучести тела.
1. Объем жидкости, вытесненной телом, называется объемным водоизмещением. Центр тяжести объемного водоизмещения совпадает с центром давления: именно в центре давления приложена равнодействующая сил.
2. Если тело погружено полностью, то объем тела W совпадает с W Т, если нет, то W < W Т, то есть P z= ρgW.
3. Тело будет плавать только в том случае, если вес тела
G Т= P z= ρgW, (2)
т. е. равен архимедовой силе.
4. Плавание:
1) подводное, то есть тело погружено полностью, если P = G т, что означает (при однородности тела):
ρgW = ρ тgW Т, откуда

где ρ,ρ Т– плотность жидкости и тела соответственно;
W– объемное водоизмещение;
W Т– объем самого погруженного тела;
2) надводное, когда тело погружено частично; при этом глубину погружения низшей точки смоченной поверхности тела называют осадкой плавающего тела.
Ватерлинией называют линию пересечения погруженного тела по периметру со свободной поверхностью жидкости.
Площадью ватерлинии называется площадь погруженной части тела, ограниченной ватерлинией.
Линию, которая проходит через центры тяжести тела и давления, называют осью плавания, которая при равновесии тела вертикальна.
13. Метацентр и метацентрический радиус
Способность тела восстанавливать свое первоначальное равновесное состояние после прекращения внешнего воздействия называют остойчивостью.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.
Интервал:
Закладка:

