Татьяна Кирюхина - Начертательная геометрия. Инженерная графика

Дисциплина «Начертательная геометрия. Инженерная графика» является фундаментальной в подготовке инженеров широкого профиля. Это одна из важнейших дисциплин общеинженерного цикла.

Проектирование, изготовление и эксплуатация машин и оборудования лесного комплекса, а также проектирование и создание объектов садово–паркового и ландшафтного строительства связаны с построением изображений: рисунков, эскизов, чертежей. Это ставит перед графическими дисциплинами ряд важных задач. Их решение обеспечит будущим специалистам знание общих методов: построения и чтения чертежей, решения разнообразных инженерно–геометрических задач, возникающих в процессе конструирования, изготовления и эксплуатации. Методы начертательной геометрии и инженерной графики необходимы для создания оборудования лесного комплекса и объектов садовопаркового и ландшафтного строительства, отвечающих современным требованиям.

Настоящие методические указания содержат задания к контрольной работе по дисциплине «Начертательная геометрия. Инженерная графика» и рекомендации по их выполнению.

Контрольная работа по начертательной геометрии и инженерной графике представляет собой чертежи, которые выполняются по мере последовательного изучения курса.

Задания контрольной работы индивидуальны. Они представлены в вариантах. Студент выполняет тот вариант задания, номер которого соответствует сумме двух последних цифр номера зачетной книжки. Если, например, шифр 31133, то номер варианта будет 6 (3+3=6).

Чертежи заданий выполняются на листах чертежной бумаги формата А3 (297х420 мм) (рисунок 1). В правом нижнем углу формата помещают основную надпись по форме 1 (рисунок 2).

Все надписи, как и отдельные обозначения букв и цифр на чертежах, должны быть выполнены стандартным шрифтом типа Б 3,5 и 5 в соответствии с ГОСТ 2.304–81. Чертежи выполняются при помощи чертежных инструментов или с применением компьютерной программы КОМРАS-3D V13.

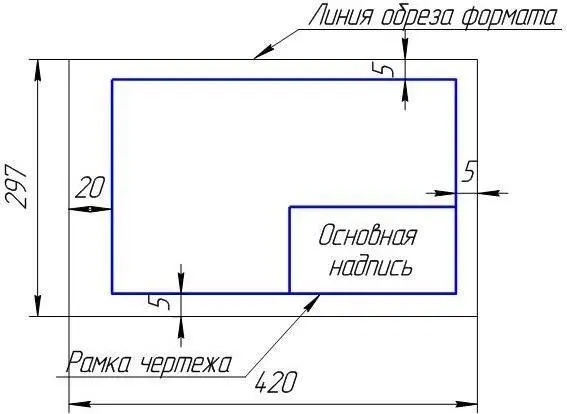
Рисунок 1 – Выделение формата А3 и выполнение рамки чертежа

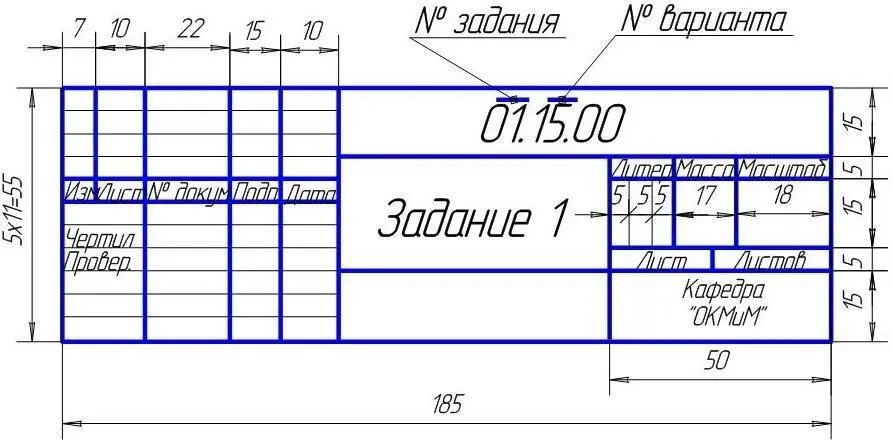
Рисунок 2 – Размеры и пример заполнения основной надписи

Толщина линий берется в соответствии с ГОСТ 2.303 – 68. Все видимые основные линии – сплошные толстые (S = 0.8 – 1,0мм), линии центровые и осевые – штрихпунктирные, толщиной от S/3 до S/2 мм, линии построений и линии связи должны быть сплошными тонкими (от S/3 до S/2 мм).

Титульный лист контрольной работы должен быть оформлен, как показано на рисунке 3.

Рисунок 3 – Оформление титульного листа контрольной работы

Контрольная работа для направления подготовки «Лесное дело» включает следующие задания:

1. Задание № 1 Способы преобразования ортогональных проекций.

2. Задание № 2 Тени в ортогональных проекциях.

3. Задание № 3 Проекционное черчение.

4. Задание № 4 Чтение и деталирование сборочного чертежа.

Цель. Получение основ определения истинной величины отрезков и плоских фигур и основ преобразования ортогональных проекций различными способами.

Содержание. Задание выполняется на листе чертежной бумаги формата А3 (297x420 мм) после предварительного решения задач на черновике.

Координаты точек А, В, С, D к решению задач № 1.1, 1.2, 1.3 приведены в приложении А. Образец оформления задания показан на рисунке 7.

Задача 1.1. Определить расстояние от точки А до плоскости треугольника ВСД, используя метод прямоугольного треугольника.

Указания. Для определения расстояния от точки А до плоскости треугольника ВСD рекомендуется следующий план решения:

1. По координатам точек А, В, С, D строим проекции треугольника ВСD и точки А в соответствии с рисунком 4;

2. Проводим в треугольнике горизонталь В1 (В/1/ – горизонтальная проекция, В//1//– фронтальная проекции) и фронталь С2 (С/2/ – горизонтальная проекция, С//2// фронтальная проекция);

3. Из точки А на плоскость треугольника опускаем перпендикуляр в соответствии с правилом « Прямая перпендикулярна к плоскости проекции, если её фронтальная проекция перпендикулярна к фронтальной проекции фронтали, горизонтальная проекция прямой перпендикулярна к горизонтальной проекции горизонтали ». В нашем примере из точки А// опускаем перпендикуляр на проекцию С// 2// и из точки А/ на проекцию В/ 1/;

4. Находим точку К пересечения перпендикуляра с плоскостью треугольника:

а) через перпендикуляр, опущенный из точки А на плоскость треугольника, проводим вспомогательную плоскость частного положения. В примере проведена горизонтально – проецирующая плоскость α (ее следы h / οαи f // οα) через горизонтальную проекцию перпендикуляра;

б) находим линию пересечения вспомогательной плоскости с треугольником ВСД. В нашем примере линия 3 – 4 (3/4/ – горизонтальная проекция, 3//4// – фронтальная проекция);

в) определяем точку встречи перпендикуляра с плоскостью треугольника ВСD. Она находится на пересечении проекций перпендикуляра и линии пересечения 3 – 4 плоскостей (К/ – горизонтальная проекция, К// фронтальная проекция). Отрезки А//К// и А/К/ являются соответственно фронтальной и горизонтальной проекциями расстояний от точки А до плоскости треугольника.

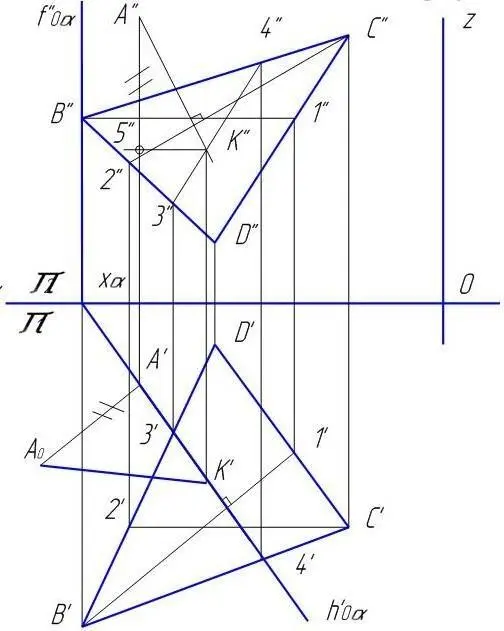
Рисунок 4 – Образец выполнения задачи № 1.1

5. Для определения истинной величины расстояния от точки А до плоскости используем способ прямоугольного треугольника. В нашем примере из точки А/ восставляем перпендикуляр и на нем откладываем отрезок А//5//=А 0А/ и обозначаем точкой А 0. Соединяем А 0с точкой К/. Отрезок А 0К/ является истинной величиной расстояния от точки А до плоскости треугольника.

Задача 1.2 Определить истинную величину треугольника ВСД методом вращения около одной из главных линий (горизонтали или фронтали).

Указания. Порядок решения задачи 1.2 показан на рисунке 5.

1. Построим проекции треугольника ВСD по их координатам.

2. Выберем ось вращения – горизонталь или фронталь в треугольнике (фронтальная проекция фронтали или горизонтальная проекция горизонтали). В примере взята фронтальная проекция фронтали С//1//.

3. Для получения истинной величины треугольника ВСD повернем его относительно оси в положение, параллельное фронтальной плоскости проекции. В примере точки оси С//1// треугольника остаются неподвижными, все остальные точки совершают поворот относительно оси по радиусам.