СССР Внутренний Предиктор - Мертвая Вода Том 2

Формально математически это означает, что если в n -мерном пространстве есть две точки, а объект необходимо перевести из одной из них в другую, то даже если существует некоторое множество равновозможных траекторий и время перевода объекта по любой из них - одно и то же, то эти траектории всё же управленчески не эквивалентны. Трёхмерный случай, иллюстрирующий эту неэквивалентность, показан на рис. 7.

На рис. 7 « 0 x 1x 2x 3 » - пространство параметров, каждый из которых является мерой одной из трёх частных ошибок управления в составе трехмерного вектора ошибки управления. То есть идеальному режиму управления соответствует начало координат. Радиус-вектор, идущий сплошной линией из начала координат, - вектор ошибки управления в момент времени t = 0. Траектории, определяемые последовательностью положений: t = 0, t = t 1, t = t 2, t = t 3 и t = 0, t = t1 1, t = t1 2, t = t1 3= t 3 - ведут из одной и той же точки в одно и то же начало координат и переход по любой из них длится одинаковое время t 3 . Выбор переходного режима (траектории) субъективно произволен, но первая траектория - оптимальна при упорядоченности вектора целей управления ( x 1, x 2, x 3 ), вторая - оптимальна при упорядоченности ( x 3, x 2, x 1 ). В реальном процессе упорядоченность параметров в векторе целей, воистину принятая в управление, выражается в порядке исчезновения частных ошибок управления (обнуления компонент вектора ошибки), вне зависимости от деклараций о благих намерениях управленцев.

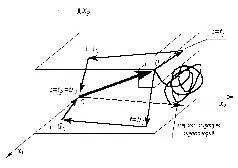
Рис. 7. Зависимость оптимальной траектории перевода объекта от упорядоченности одного и того же набора контрольных параметров в векторе целей управления

Предположим, что на рис. 7: x 1 - мера недостачи возможностей в получении образования подрастающим поколением; x 2 - мера недостачи в питании, одежде, жилье, инфраструктурах; x 3 - мера дефицита в роскоши и продукции деградационно-паразитического спектра потребностей. В силу действия неформализуемых взаимно изключающих обусловленностей параметров x 1 и x 3 при упорядоченности ( x 3, x 2, x 1 ), система вряд ли пройдёт по соответствующей такой упорядоченности траектории далее половины пути. Скорее всего, вследствие действия не формализованных в модели факторов, она уклонится в иной ошибочный режим, показанный пунктирным радиус-вектором, идущим из начала координат, который возможно не будет устойчивым балансировочным режимом. Именно на этот путь ступили “демократизаторы” и хотят вести по нему народ.

Тому, кто себе в лоб забил алкогольно-никотиновый кол, лично непотребно образование, новое знание, поскольку оно - в тягость наркотически угнетённому. А его потомство, вследствие вероятностно предопределённых генетических нарушений, как в биомассе организма, так и в изкалеченной и подавленной психике, возможно не сможет освоить и те знания и культурные навыки, что были достоянием предков. Это приведёт к падению культуры производства и уронит спектры производства и потребления.

“Саморегуляция” рынка без разделения демографически обусловленного и деградационных спектров будет выглядеть на рис. 7 по этим информационным причинно-следственным обусловленностям как хаотичное мельтешение ненулевого радиус-вектора в пространстве параметров, относительно какого-то среднестатистического положения, управляемого внесистемными факторами. “Саморегуляция” такого рода показана на рис. 7 как клубковидная “каракуля”.

Оптимизация каждого из множества производственных циклов D T вне объемлющей задачи оптимизации по минимуму времени переходного процесса изчерпания недостаточности демографически обусловленного спектра потребления - изначально методологически несостоятельная задача, поскольку это - “оптимальный” шаг неизвестно куда. Но и оптимизация переходного макроэкономического процесса - лишь частная задача в процессе перехода к жизни общества в ладу с объемлющей его биосферой.

Теперь разсмотрим метод динамического программирования , поскольку хотя и было показано, что алгоритмы решения задачи об оптимальном наведении средств поражения на цель в нынешней цивилизации не могут не существовать, тем не менее необходимо содержательно обсудить ещё некоторые “само собой” разумеющиеся очевидности, касающиеся оптимального выбора траекторий многопараметрических переходных процессов.

Формализованный выбор оптимальной в некотором смысле траектории в n -мерном пространстве возможен, в частности на основе изпользования аппарата “динамического программирования”. Термин “динамическое программирование”, также как и термин “линейное программирование”, - прижившийся в Русском языке подстрочник, мало что говорящий о существе самого метода.

Аппарат динамического программирования позволяет решать задачи многопараметрической оптимизации в тех случаях, когда в силу разного рода объективно-математических причин (дискретность ограничений, нелинейности, нарушение свойства выпуклости и т.п.) аппарат линейного программирования неработоспособен. Вполне понятно, что он тоже не изучался и не изучается в большинстве вузовских курсов СССР и России на специальностях, в которых владение им придаёт квалификации специалистов КАЧЕСТВЕННО более высокий уровень.

В изложении существа метода динамического программирования мы опираемся на книгу “Курс теории автоматического управления” (автор Палю де Ла Барьер: французское издание 1966 г., русское издание - “Машиностроение”, 1973 г.), хотя и не повторяем его изложения. Отдельные положения взяты из курса “Исследование операций” Ю.П.Зайченко (Киев, “Вища школа”, 1979 г.).

Метод динамического программирования работоспособен, если формальная интерпретация реальной задачи позволяет выполнить следующие условия:

1. Разсматриваемая задача может быть представлена как N -шаговый процесс, описываемый соотношением:

X n + 1= f(X n,U n, n) , где n - номер одного из множества возможных состояний системы, в которое она переходит по завершении n -ного шага; X n - вектор состояния системы, принадлежащий упомянутому n -ному множеству; U n - управление, выработанное на шаге n (шаговое управление), переводящее систему из возможного её состояния в n -ном множестве в одно из состояний ( n + 1 )-го множества. Чтобы это представить наглядно, следует обратиться к рис. 4, о котором речь пойдёт далее.