Жюль Верн - С Земли на Луну прямым путем за 97 часов 20 минут. Вокруг Луны (сборник)

– Ты хочешь сказать, – перебил Барбикен, – до той нейтральной точки, где силы земного и лунного притяжения одинаковы, потому что с этой точки, которая находится почти на девяти десятых всего расстояния между обеими планетами, снаряд полетит на Луну сам собой вследствие собственной тяжести.

– Ну да, именно это я и имел в виду, – сказал Мишель. – Но как же все-таки они вычислили эту скорость?

– Ничего нет легче.

– А ты сумел бы сам провести это вычисление?

– Ну разумеется. Мы с Николем вычислили бы эту скорость и сами, если бы справка обсерватории не избавила нас от этого труда.

– Подумать только, – вздохнул Мишель. – А я бы не мог решить этой задачи даже под страхом смертной казни.

– Потому что ты не знаешь алгебры, – спокойно ответил Барбикен.

– Эх вы, «иксоеды»! Вы, думаете, сказали: «Алгебра», и этим все объяснили!

– Мишель, – сказал Барбикен, – ты, надеюсь, не станешь отрицать, что нельзя ковать без молота и ли пахать без плуга?

– Не стану, конечно.

– Ну, так алгебра – такое же орудие, как соха или плуг, и орудие весьма полезное для тех, кто умеет с нею обращаться.

– Не может быть.

– Сущая правда.

– А ты согласен воспользоваться этим орудием тут же при мне? Если тебе, конечно, не скучно.

– Разумеется.

– И показать мне, как вычислить начальную скорость нашего снаряда?

– Да, дорогой друг. Приняв в расчет все известные условия задачи: расстояние от центра Земли до центра Луны, радиус Земли, массу Земли, массу Луны, я могу с точностью установить начальную скорость нашего снаряда, и при этом с помощью самой простой формулы.

– Какая же это формула?

– А вот увидишь. Но только я не стану вычеркивать кривой, описанной нашим снарядом между Луной и Землей, учитывая их относительное движение вокруг Солнца. Предположим, что обе планеты неподвижны. Этого будет совершенно достаточно.

– Почему же?

– Потому что именно так решаются задачи, называемые «задачами трех тел», интегральный же метод для решения таких задач еще недостаточно разработан.

– Скажите, пожалуйста, – насмешливо произнес Мишель Ардан, – стало быть, математики еще не сказали своего последнего слова!

– Ну, разумеется, нет, – ответил Барбикен.

– Ну что ж! Авось лунные жители довели интегральное исчисление до большего совершенства, чем вы! А кстати, что такое интегральное исчисление?

– Этот способ, противоположный дифференциальному исчислению…

– Благодарю покорно!

– Другими словами, это исчисление, дающее нам конечные величины, дифференциалы которых нам известны.

– Вот это по крайней мере понятно! – воскликнул Мишель с видом полного удовлетворения.

– А теперь, – сказал Барбикен, – дай мне кусочек бумаги, огрызок карандаша, и через полчаса я покажу тебе нужную формулу.

С этими словами Барбикен принялся за вычисления. Николь продолжал изучать в окно необозримые межпланетные пространства, предоставив Мишелю заботу о завтраке.

Не прошло и получаса, как Барбикен, подняв голову, показал Ардану бумажку, исписанную алгебраическими знаками, среди которых выделялась следующая формула:

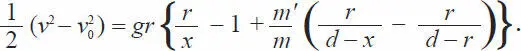
– Что же это значит? – спросил Мишель.

– Это значит, – ответил Николь, – что одна вторая v в квадрате минус v нулевое в квадрате равно gr , помноженное на r , деленное на х , минус единица плюс m прим, деленное на m , умноженное на r , деленное на d минус х , минус r , деленное на d минус r …

– Икс плюс игрек на закорках у зета и верхом на р , – расхохотался Мишель. – И все это тебе понятно, капитан?

– Ничего нет понятнее.

– Ну еще бы! – сказал Мишель. – Да ведь это же ясно с первого взгляда; теперь мне больше ничего не требуется.

– Вечно ты издеваешься! – вмешался Барбикен. – Захотел алгебры, ну и получай.

– Пусть уж лучше меня повесят!

– В самом деле, – сказал Николь с видом знатока, читая формулу. – Мне кажется, эта формула совершенно правильна. Это интеграл уравнения действующих сил, и я не сомневаюсь, что она приведет к искомому результату!

– Но я тоже хочу хоть что-нибудь понять! – вскричал Мишель. – Я готов отдать за это десять лет жизни… Николя.

– Ну так послушай, – начал Барбикен. – Половина v квадрат минус v нулевое в квадрате – это формула, дающая нам полувариацию действующей силы.

– Ну допустим. А Николь тоже понимает, что это значит?

– Конечно, Мишель, – ответил капитан. – Все эти, кажущиеся тебе каббалистическими, знаки составляют собой простой, самый точный и логичный язык для тех, кто им владеет.

– И ты полагаешь, Николь, – сказал Мишель, – что при помощи таких иероглифов, еще более непонятных, чем египетские «ибисы», ты сможешь найти начальную скорость, которую следовало сообщить снаряду?

– Безусловно, – ответил Николь. – При помощи этой формулы я смогу даже сказать тебе, с какой скоростью летит снаряд в любой точке пространства.

– Честное слово?

– Честное слово.

– Подумать только, ты, значит, ученый не хуже нашего председателя!

– Нет, Мишель. Барбикен сделал как раз самое трудное. Он нашел уравнение, определяющее все условия задачи. Остальное – вопрос арифметики и требует только знания четырех правил.

– Ну это действительно пустяки! – ответил Мишель Ардан, хотя ни разу в жизни не одолел ни одной задачи на сложение и называл эти упражнения «китайскими головоломками, позволяющими получать бесконечно разнообразные итоги».

Барбикен, однако, уверял, что и Николь, поразмыслив, смог бы самостоятельно найти ту же формулу.

– Не знаю, – возразил Николь, – чем больше я ее изучаю, тем больше она меня восхищает.

– А теперь, – сказал Барбикен, обращаясь к своему невежественному другу, – слушай. Ты поймешь, что все эти буквы имеют определенные значения.

– Слушаю, – смиренно сказал Мишель.

– d означает расстояние между центрами Земли и Луны, – сказал Барбикен. – Эти точки нам нужны для вычисления сил притяжения.

– Понятно.

– r – радиус Земли.

– Радиус… Допустим.

– m – масса Земли, а m прим – это масса Луны. Эти величины приняты в формуле потому, что притяжение тел пропорционально их массам.

– Понимаю.

– g – сила тяжести, скорость, приобретаемая телом в течение секунды при падении на поверхность Земли. Ясно?

– Как божий день!

– Буквой х я обозначил то переменное расстояние, которое отделяет нас от центра Земли, а v – скорость снаряда при данном расстоянии.

– Прекрасно!

– Наконец, скорость снаряда по выходе из атмосферы обозначим v нулевое.

– Правильно, – сказал Николь, – до этой точки и следовало вычислять скорость, так как известно, что начальная скорость в полтора раза больше той, которую снаряд сохранил при выходе из атмосферы.