Array Коллектив авторов - Политическая наука №1 / 2018

Следуя примеру Дойча, я обратился к изучению некоторых взаимосвязей, которые можно считать своего рода законами человеческой активности. Однако мой подход, который я принес с собой из физики, не был подхвачен коллегами, а скорее вызвал сопротивление. Вот почему премия Карла Дойча – приятный сюрприз для меня. Она означает, что я могу еще активнее заняться реализацией своей второй мечты – превращением социальных исследований в настоящую науку. Не внедрять математический аппарат, как порой превратно полагают, а продвигать логические модели. Но сначала немного слов о том, как я обратился к социальным исследованиям.

Однажды, когда мне было одиннадцать лет и я пас коров во время Второй мировой войны, мне подумалось вот что. Представьте, что сто солдат противостоят пятидесяти солдатам в открытом поле. Кто угодно может застрелить кого угодно из противоположного лагеря. Предположим, что их орудия и навыки равны. Сколько из 100 останется в живых, после того как 50 других будут уничтожены? Я подозревал, что потери превосходящей силы будут довольно малы. Я проделал некоторые расчеты в уме, но они оказались слишком сложными, а у меня с собой не было бумаги. Поэтому мне пришлось сдаться. Однако это означало, что в глубине души у меня созрело стремление использовать количественные логические модели для анализа социальных проблем.

Много позже я вспомнил эту задачу. Я быстро составил систему двух дифференциальных уравнений и решил их. Результат – целых 87 из 100 выживут. И что же, опубликовал ли я этот результат? Нет, не тут‐то было. Некий Ланчестер уже разработал эти уравнения в 1916 г., т.е. задолго до моего рождения [Lanchester, 1956].

Подобно Карлу Дойчу, мы с семьей бежали от тоталитарного режима в Восточной Европе. В конце концов я оказался в Северной Америке. По дороге я окончил среднюю школу в городе Марракеше (Марокко). Степень бакалавра ядерной физики я получил в Университете Торонто, а степень доктора физических наук – в Университете Делавера. Я публиковался в области ядерной физики и физики твердых тел [Taagepera, Nurmia, 1961; Taagepera, Storey, McNeill, 1961; Taagepera, Williams, 1966], но больше работал с текстильными волокнами в промышленной лаборатории (Pioneering Laboratory, DuPont de Nemours Experimental Station). Однако меня по-прежнему волновало то, что случилось с моей семьей и моей страной в ходе коллизий мировой политики. Поэтому я стал посещать вечерние курсы по политологии и в конце концов получил степень магистра международных отношений.

Во время обучения я обратил внимание на так называемый кубический закон выборов в англосаксонских странах. Это отношение применимо к двум основным партиям в выборах по мажоритарной системе относительного большинства с одномандатными округами. Оно отражает тот факт, что большая партия имеет изрядный бонус – ее доля мест больше, чем доля голосов. Но насколько больше? Просто сказать «больше голосов, больше мест» – это примитивная наука. Направления изменения недостаточно. Чтобы считаться наукой, мы должны делать взаимосвязи количественными. Это означает, что мы должны задаться вопросом о том, насколько большую долю мест получит партия с заданной долей голосов.

Кубический закон выборов это и делает. Он соединяет отношение мест двух партий, А и В, и отношение их голосов. Отношение мест примерно равно кубу отношения голосов S A/S B =( V A/V B ) 3. Например, если проценты голосов близки к 60:40, то так называемый кубический закон говорит, что проценты мест будут различаться как 77:23.

Эта взаимосвязь нелинейна. Она кривообразна, причем довольно сложным образом, что навязано ее логикой. Почему я обращаю на это внимание? Потому что слишком много социальных исследователей, видимо, верят, что все количественные взаимосвязи линейны. Никто из них не верит в плоскую Землю, но они верят в прямые линии. Суровая реальность состоит в том, что линейные взаимосвязи очень редки в естественных науках, и не говорите мне, что социальные взаимосвязи проще. Вот где социальные науки производят много мусора, создавая множество призрачных линейных взаимосвязей.

Но вернемся к так называемому кубическому закону. Это не был на самом деле закон, а всего лишь эмпирическая закономерность. Чтобы квалифицировать ее как закон в строгом научном смысле, мы должны также иметь обоснование, почему взаимосвязь должна иметь ту форму, которую имеет, почему она не может быть никакой другой формы. Вот что меня озадачивало. И ответ был найден.

Чтобы объяснить феномен, попытайтесь поместить его в более широкий контекст. Здесь взаимосвязь необязательно кубическая. Результат зависит от общего количества мест. Действительно, там, где на кону только одно место, как на президентских выборах, отношение голосов 60:40 приводит к отношению мест, равному не 77:23, а 100:0.

Позвольте, могут воскликнуть некоторые политологи, неужели вы, глупые физики, не знаете, что президентские и парламентские выборы – это совершенно разного рода вещи? Вы не можете поместить их в одну модель. Я встречаю такие заблуждения снова и снова, и это мешает политологии стать наукой. О да, я могу применять одну и ту же модель к парламентским и президентским выборам. Если бы я ошибался, то количественная логическая модель просто бы не работала, но мое расширение кубического закона работает. Это подтверждает, что в некоторых отношениях президентские выборы на основе относительного большинства (by plurality) – лишь предельный случай парламентских выборов по тем же правилам относительного большинства в одномандатных округах 4 4 По некоторым другим аспектам президентские выборы отличаются от парламентских, потому что экстремальные случаи всегда необычны. Одной из целей Шугарта и Таагеперы [Shugart, Taagepera, 2017] является определение количественных аспектов, по которым можно выяснить, где и как начинаются отличия президентских выборов от парламентских. . Позднее я опубликовал свою модель в виде «уравнения мест и голосов» [Taagepera, 1973]:

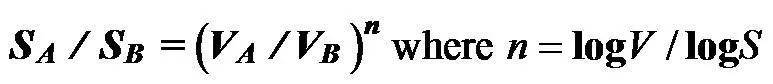
Здесь V – общее количество голосов, S – общее количество мест. Сейчас я называю эту модель законом сокращения меньшинства, потому что она может применяться более широко, за пределами выборов. Например, она описывает соотношение женщин и мужчин среди ассистентов и профессоров [Taagepera, 1994]. Рассмотренный под другим углом, этот закон также создает паттерн, по которому Европейский союз распределил места в Европейском парламенте между странами [Taagepera, Hosli, 2006].

Сокращение меньшинства выражается в так называемом кубическом законе, когда количество мест в ассамблее составляет кубический корень количества избирателей, соответствующего численности населения. К своему удивлению, я нашел, что это так в большинстве демократических стран. Путем проб и ошибок страны обнаружили, что кубический корень численности населения – это наиболее эффективный размер законодательного собрания. То есть страна с 8 миллионами населения обычно имеет представительное собрание из 200 человек, так как 200 х 200 х 200 = 8 миллионов.