Константин Гулин - Социально-экономическое неравенство населения региона

Выделение однородных подвидов домохозяйств по различным критериям (размер и тип домохозяйства, уровень доходов и потребления и др.) является основной задачей, которую решают при анализе социального расслоения. Обычно степень социальной дифференциации населения определяется как разница в показателях доходов в расчете на члена домохозяйства или домохозяйство в целом. Различия в оценках степени расслоения, получаемых в зависимости от этого, обусловлены различиями в размерах домохозяйств с разным уровнем дохода. Оценки дифференциации домохозяйств по душевым доходам важны в связи с тем, что общие потребности семьи, естественно, растут с увеличением ее размера, но не пропорционально ему из-за относительной экономии.

Распределение домохозяйств (населения) по размеру среднего на домохозяйство (душу) дохода является главной характеризуемой особенностью дифференциации населения по уровню материального благосостояния.

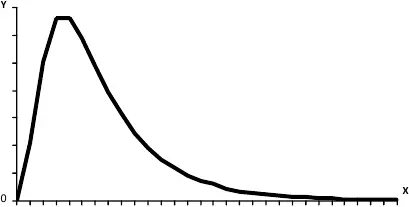
В 30-е гг. XX в. французский экономист Р. Жибра доказал, что распределение семей и их членов по доходу имеет правостороннюю асимметрию и выравнивается по логарифмическому нормальному распределению. Логарифмическое нормальное (логнормальное) распределение – это распределение случайной величины (х), логарифм которой (lnx) подчинен нормальному закону распределения. При малой дисперсии логнормальное распределение близко к нормальному. Логнормальное распределение определяется двумя параметрами: средним логарифмом доходов (lnX o) и средним квадратическим отклонением логарифмов доходов (σ) (рис. 1.2) . Функция логнормального распределения рассчитывается по формуле:

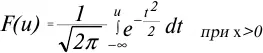
Рисунок 1.2. Логнормальное распределение

Распределение домохозяйств (населения) по уровню дохода позволяет рассчитывать децильные (разбивающие всю совокупность на 10 интервалов по 10 % единиц наблюдения в каждом интервале) и квинтильные (на пять интервалов по 20 % единиц) интервалы и интервалы с заданными (фиксированными) границами уровней дохода и численности населения и домохозяйств в них. Для различных потребностей анализа возможно исследовать совокупность домохозяйств, ранжированную по уровню среднего на домохозяйство дохода и среднедушевого дохода, или исследовать совокупность членов домохозяйств, ранжированную по уровню среднедушевого дохода или по уровню дохода на домохозяйство.

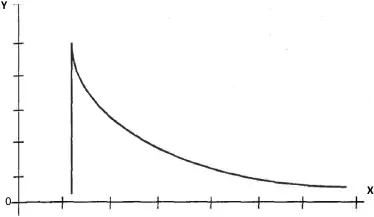
При экономическом анализе характера распределения доходов в обществе широко используется распределение В. Парето, которое показывает распределение доходов населения между его группами в зависимости от их величины (рис. 1.3) . На оси Х показаны доходы, а на оси Y – число домохозяйств или лиц, имеющих доход равный или больше определенной границы (а). В. Парето эмпирическим путем получил гиперболы, описываемые формулой:

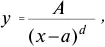
где: а – минимальный доход; А и d — положительные параметры.

Рисунок 1.3. Распределение В. Парето

Социально-экономическую дифференциацию измеряют не только через оценки количества домохозяйств (населения) в группах с разным уровнем доходов. Оцениваются и другие параметры домохозяйств (населения) с разным уровнем материального благосостояния: тип и размер домохозяйства, характеристики его членов (пол, возраст, занятость), структура и объем доходов и расходов, уровень потребления продуктов питания и др. Эти показатели рассчитываются на домохозяйство или на душу по децильным, квинтильным интервалам и интервалам с фиксированными границами уровня доходов.

Для характеристики степени расслоения часто пользуются показателем превышения доходов 10 % населения, имеющего самые высокие доходы, и 10 % населения с самыми низкими доходами. Этот показатель, называемый коэффициентом фондов (Kf) , представляет собой отношение средних значений признака в границах верхнего и нижнего децилей:

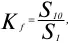
где S 10 – суммарный доход, который приходится на 10 % населения с самыми высокими доходами; S 1 – суммарный доход, который приходится на 10 % населения с самыми низкими доходами.

Коэффициент фондов, рассчитанный по данным ряда распределения домохозяйств (населения) по уровню среднего на домохозяйство (на члена домохозяйства) дохода, показывает, во сколько раз среднедушевой доход 10 % наиболее высокодоходного населения (домохозяйств) больше, чем доход 10 % населения (домохозяйств) с наименьшими доходами. Помимо того, что сопоставляются доходы этих групп домохозяйств, оценивается разница в уровнях душевого потребления продуктов питания, непродовольственных товаров и услуг, в объеме и структуре доходов и расходов, среднем размере домохозяйств, их составе и других показателях. В этом случае коэффициент фондов показывает, как отличается в среднем уровень потребления, расходов и т. п. у 10 % самого богатого населения от соответствующих показателей у 10 % самых бедных.

В качестве одного из показателей степени дифференциации населения по уровню доходов в социально-экономической статистике используется индекс концентрации доходов, или коэффициент

Джини (К L ) , отражающий характер распределения всей суммы доходов населения между отдельными его группами. Его величина изменяется от 0 до 1. При равномерном распределении доходов коэффициент принимает значение 0. Чем ближе значение показателя расположено к 1, тем более неравномерно распределены доходы в обществе. Для расчета описанного коэффициента применяется формула:

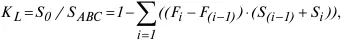
где ( F i – F i-1 ) – доля населения, относящаяся к i-му интервалу; S i-1 , S i – доля суммарного дохода, приходящаяся на начало и конец i-го интервала.

Расчет коэффициента Джини производится на основании данных о распределении домохозяйств (населения) по уровню среднего на домохозяйство (члена домохозяйства) дохода. После того как вся совокупность получателей доходов будет поделена на 5 равных квинтильных групп, определяется, какой долей дохода владеет каждая группа домохозяйств (населения). По полученным накопленным итогам строится кривая Лоренца, которая представляет собой графическое изображение уровня концентрации явления. Для изображения кривой Лоренца на осях координат с процентной шкалой от 0 до 100 откладываются кумулятивные (накопленные) итоги распределения: на горизонтальной оси – квинтили получателей доходов, на вертикальной – квинтили полученных доходов. Кривая Лоренца строится путем соединения точек, соответствующих кумулятивным процентным долям доходов, полученных квинтильными группами населения (рис. 1.4) .