Томас Кун - После «Структуры научных революций»

Приняв к сведению эту головоломку, начинаешь понимать, что для Вольты и его последователей отдельный элемент состоит из двух металлических пластинок, соединенных вместе. Источником силы является контакт металлов, в котором Вольта обнаружил источник электрического напряжения. Тогда роль жидкости состоит просто в том, чтобы связывать один элемент с другим, не создавая потенциала, способного нейтрализовать первоначальный эффект. Изучая текст Вольты дальше, приходишь к выводу, что свое новое открытие он относил к электростатике. Биметаллическое соединение оказывается конденсатором, или лейденской банкой, которая заряжает саму себя. Тогда столбик из отдельных элементов представляется как ансамбль или «батарея» самозаряжающихся лейденских банок. Вот так термин «батарея» начинает применяться к электричеству. Подтверждением может служить верхняя часть рисунка Вольты, иллюстрирующая структуру, которую он называет «связкой чашек».

Рис. 1

Хотя этот рисунок очень похож на диаграммы в современных элементарных учебниках, здесь опять-таки имеется странность. Почему чашки на двух концах диаграммы содержат только один кусок металла? Почему Вольта включает две половинки элемента? Ответ прежний. Для Вольты чашки являются не элементами, а простыми емкостями для жидкости, связывающей элементы. Сами элементы являются биметаллическими подковообразными прутиками. Незанятые места в крайних чашках мы должны представлять себе как связанные дополнительным прутом. В диаграмме Вольты нет половинок элементов.

Как и в предшествующем примере, такой взгляд на электрическую батарею приводит к разнообразным следствиям. Как показано на рис. 2, например, переход от представлений Вольты к современным сохраняет направление потока. Современное изображение элемента (рис. 2, в) можно получить из диаграммы Вольты (рис. 2, а) посредством перемещения левой пластины по кругу (рис. 2, б). При этом то, что было внутренним потоком, становится внешним, и наоборот. В диаграмме Вольты внешний поток идет от черной пластины к белой, поэтому черная пластина является положительной. В современном изображении и направление потока, и полярность противоположны.

Концептуально гораздо более важным является изменение понимания источника тока. Для Вольты существенным элементом ячейки и источником тока было соприкосновение металлических пластин. Когда ячейка была вывернута и жидкость стала соприкасаться с двумя металлическими пластинами, источником тока стал химический эффект этих взаимодействий.

Когда обе эти точки зрения были сопоставлены, то первая получила известность как контактная теория, а вторая – как химическая теория электрической батареи.

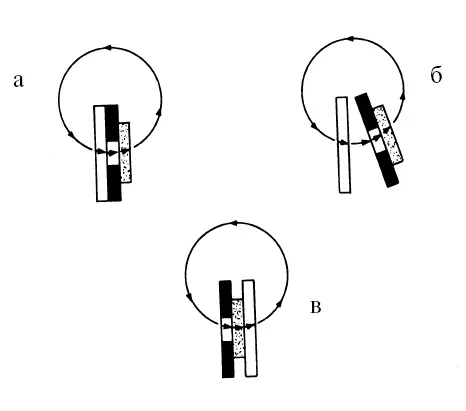
Рис. 2

Это лишь наиболее очевидные следствия электростатического понимания электрической батареи, но имеются и другие. Например, концепция Вольты не замечает концептуальной роли внешней цепи. То, что представляется нам внешней цепью, для Вольты является путем разряда, подобного разряду, который разряжает лейденскую банку. Поэтому ранние рисунки батареи не показывают внешней цепи, если нет стороннего вмешательства, например, электролиза или нагревания проволоки. Не раньше 1840-х годов в книгах по электричеству начинают появляться современные изображения электрических ячеек. На них уже можно видеть либо внешнюю цепь, либо указания на ее присутствие [10](см. рис. 3 и 4).

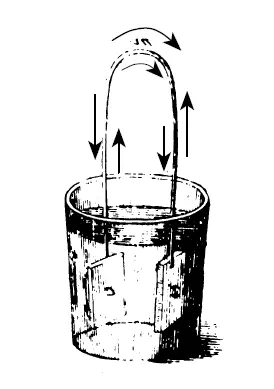
Рис. 3

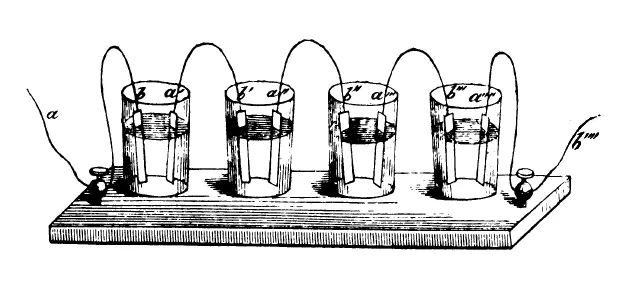
Рис. 4

Наконец, электростатическое истолкование электрической батареи ведет к отличному от современного пониманию электрического сопротивления. В тот период существовала электростатическая концепция сопротивления. Для изоляционного материала данного сечения сопротивление измеряли посредством толщины, которая позволяла ему не разрушаться и оставаться изолятором при данном напряжении. Для проводника определенного сечения сопротивление измеряли посредством той его длины, при которой он не расплавлялся, когда через него пропускали ток.

Сопротивление можно измерять таким способом, но результаты измерения несовместимы с законом Ома. Для получения этих результатов нужно представить электрическую батарею в виде гидродинамической модели. Здесь сопротивление становится похоже на трение протекающей воды о стенки трубы. Включение сюда закона Ома потребовало некумулятивного изменения подобного рода, поэтому для многих людей его принятие оказалось очень трудным. Это дает нам стандартный пример важного открытия, которое первоначально отвергалось или игнорировалось.

На этом я заканчиваю рассмотрение второго примера и перехожу к третьему, более современному и несколько более сложному.

До сих пор идут споры об источниках квантовой теории [11]. Главный предмет обсуждения – работа Макса Планка по проблеме черного тела – работа, ход которой можно представить следующим образом. Сначала Планк решил проблему черного тела в 1900 г., используя классический метод, разработанный австрийским физиком Людвигом Больцманом. Через шесть лет в его выводе была обнаружена небольшая, но принципиальная ошибка, затрагивающая один из важнейших элементов этого вывода. Планк исправил решение, но при этом был вынужден радикально отойти от традиции. В конечном счете этот разрыв с традицией привел к перестройке значительной части физики.

Начнем с Больцмана, который представлял себе газ как совокупность множества крохотных молекул, быстро движущихся в замкнутом сосуде и сталкивающихся друг с другом и со стенками сосуда. Из работ других физиков Больцман знал, какова средняя скорость молекул (точнее, каков в среднем квадрат их скорости). Но многие молекулы двигались, конечно, с меньшей, чем средняя, скоростью, а какие-то из них двигались быстрее. Больцман хотел установить, какая часть молекул двигалась с ½ от средней скорости, какая часть – с 4/ 3средней скорости и так далее. Ни сам вопрос, ни ответ, который он нашел, не были открытием. Однако Больцман пришел к ответу новым путем, исходя из теории вероятностей, и этот путь имел фундаментальное значение для Планка.

Для нас здесь важен лишь один аспект метода Больцмана. Он рассматривал общую кинетическую энергию молекул Е. Чтобы использовать теорию вероятностей, он мысленно разделял эту энергию на маленькие кусочки, или элементы, величины г, как показано на рис. 5. Затем воображал случайное распределение молекул среди этих кусочков, вытаскивая пронумерованные бумажки из урны, чтобы установить место каждой молекулы, а потом исключая все распределения с общей энергией, отличной от Е . Например, если первая молекула попадала в последний отрезок (энергия Е ), то единственно приемлемым распределением оказывалось бы такое, при котором все другие молекулы попадали в первый отрезок (энергия о).