Майкл Эдлесон - Усреднение ценности. Простая и надежная стратегия повышения доходности инвестиций на фондовом рынке

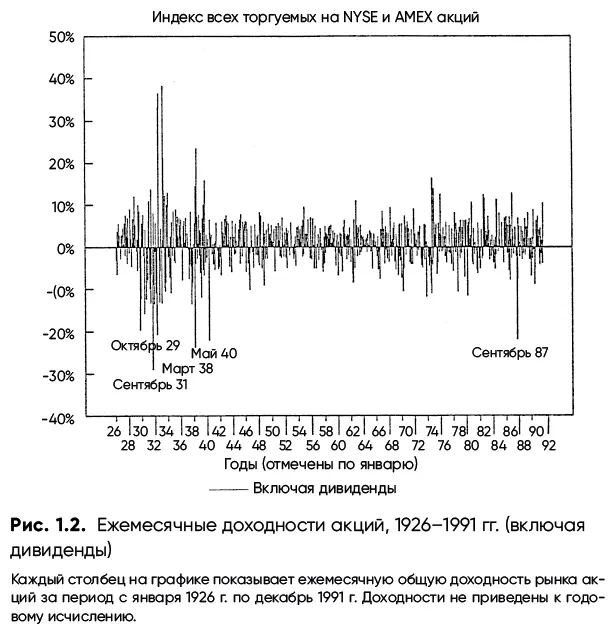
На рис. 1.2 показана общая доходность (рост капитала плюс дивиденды) за каждый месяц на протяжении 66 лет. Хотя для рынка крайне необычны изменения более чем на 20 % в месяц, вы можете заметить, что такое происходило в течение этого периода около десятка раз. Среднерыночная месячная доходность составляла чуть ниже 1,0 % (0,95 % ежемесячно), или 12 % в годовом исчислении [7] Этот средний показатель 12 % не противоречит ранее приведенной ставке роста с учетом сложного процента 9,98 %. Более высокое значение (12 %) получается путем простого усреднения всех годовых доходностей периода; значение же 9,98 % демонстрирует условно-постоянный прирост, который соответствует росту начального значения до значения конечного. В этом и состоит разница между средним арифметическим и средним геометрическим значениями. Простой пример: акции стоимостью $100, которые падают до $50 (‒50 %) в первый год, а затем отскакивают (+100 %) обратно до $100 во второй год. Среднее арифметическое, или просто среднее, этих двух показателей годовых значений составляет +25 %, однако годовой темп роста с учетом сложного процента от начала ($100) до конца ($100) периода явно был нулевым. Средние арифметические значения всегда выше средних геометрических. Это означает, что средняя доходность нескольких периодов всегда будет выше, чем фактическая компаундированная доходность совокупного периода. . (См. врезку «Доходности и сложный процент».)

Каждый столбец на графике показывает ежемесячную общую доходность рынка акций за период с января 1926 г. по декабрь 1991 г. Доходности не приведены к годовому исчислению.

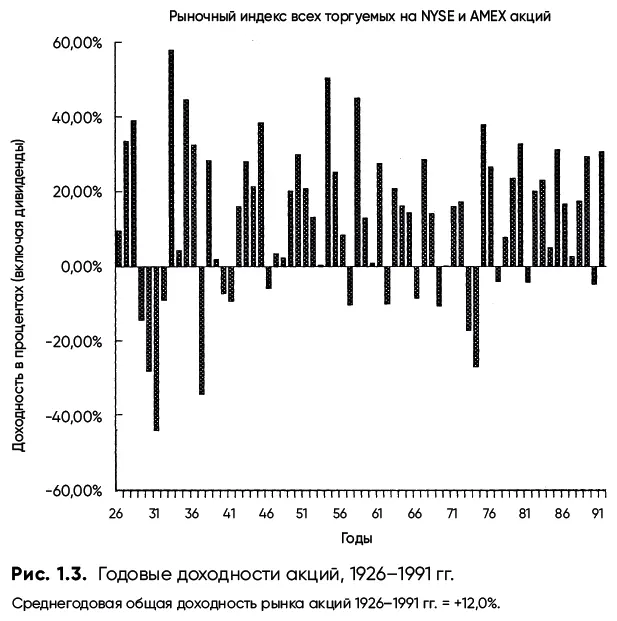
На рис. 1.3 представлены аналогичные данные, но уже не по месяцам, а по годам. Здесь легче увидеть, что рынок в целом растет, но на нем все еще присутствует волатильность, нарушающая тенденцию. Диапазон доходностей колеблется от ‒44 до +58 %, хотя со времен Второй мировой войны эти значения находятся в более узком диапазоне: от ‒28 до +51 %. Конечно, отдельные акции демонстрируют куда большую волатильность, чем рынок в целом, поэтому не стоит путать типичную рыночную доходность с данными отдельно взятой бумаги.

Доходности и сложный процент

Доходность инвестиций (возьмем, например, значение 8 %) должна быть привязана к определенному временнóму периоду. Обычно, но не всегда, используется годовая доходность. Когда мы переключаем наше внимание с одного периода на другой, нужно сделать перерасчет и для доходности.

Предположим, что общая доходность двухлетних инвестиций составила 21 %. Казалось бы, можно просто привести двухлетнюю доходность к годовой. Однако взять и разделить 21 % на 2, получив значение годовой доходности 10,50 %, будет ошибкой. Простое «усреднение» доходности игнорирует компаундирование, или сложный процент . Допустим, вы инвестировали $100 на два года и в первый год получили доход в размере 10,50 %. Это дает вам $110,50. При доходности 10,50 % во втором году вы получите $122,10 (10,50 % от $110,50 составляет $11,60). Это двухлетняя доходность 22,10 %, а вовсе не 21 %. На самом деле двухлетняя доходность 21 % эквивалентна годовой доходности 10 % ($100 + 10 % = $110; $110 + 10 % = $121; общая доходность 21 %).

Если a – это годовая доходность, то следующая формула поможет вам рассчитать доходность с учетом сложного процента за n лет:

(1 + a) n = 1 + доходность за n лет.

В приведенном выше примере a = 10 % и n = 2, поэтому:

(1 + 0,10) 2= 1,21 = 1 + доходность за n лет,

где 0,21 = 21 % = двухлетняя доходность.

Этот процесс работает и в обратном направлении, если вам нужно найти годовую доходность, имея значения доходности за более долгий период. Если взять корень n -ной степени (на калькуляторе это соответствует возведению в степень 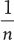), формула приобретет следующий вид:

Пример.Какая годовая ставка даcт вам 50 % доходности за пять лет?

1 + a = корень n -ной степени из (1 + 0,50) = (1,50) 0,2= 1,0845; a = 8,45 % годовых.

Эта операция также может быть использована для расчета доходности с учетом сложного процента (компаундированной доходности) на периодах, длина которых составляет менее года. С помощью формулы, данной выше, рассчитайте, какова будет ежемесячная доходность с учетом сложного процента, если годовая доходность равна 12 %? Подсказка: один месяц – это 1⁄12 года.

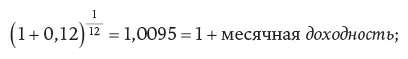
0,0095 = 0,95 % = месячная доходность.

Более общий вид формулы полезен для перевода месячных ставок в годовые. Предположим, что ваш длинный расчетный период в n раз больше вашего короткого расчетного периода. Тогда компаундированные доходности этих периодов будут связаны следующим образом:

(1 + доходность короткого периода) n = 1 + доходность длинного периода.

Предположим, вы можете зарабатывать на инвестициях 1,0 % ежемесячно. Какова окажется годовая доходность?

В этом случае доходность за короткий период составляет 0,01, а n = 12:

(1,01) 12= 1,1268 = 1 + длинная (годовая) доходность; 0,1268 = 12,68 % = годовая доходность.

Этот метод преобразования месячной доходности в годовую и наоборот наиболее корректен и используется на протяжении всей книги.

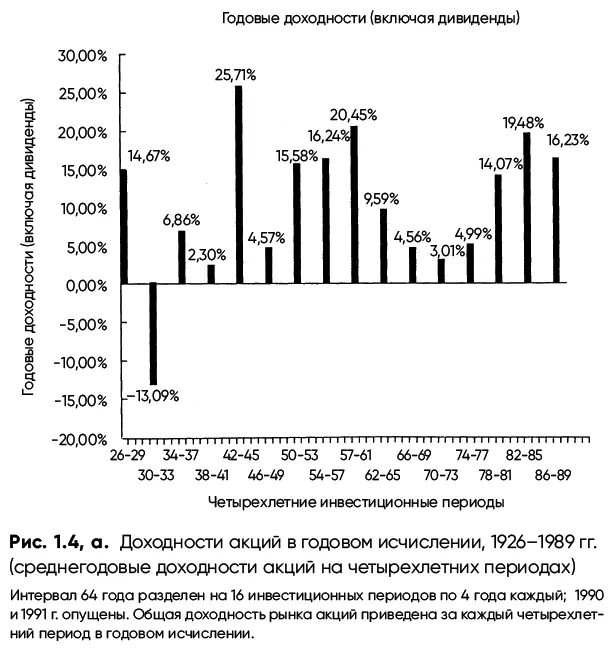
Несмотря на то, что рынок действительно является довольно рискованным местом, утверждение о том, что «время врачует раны» , применительно к нему можно назвать правдивым. Это заметно на рис. 1.4, а, где вместо однолетних мы рассматриваем четырехлетние периоды. На таком масштабе картина меняется: лишь самый тяжелый период в экономике, пришедшийся на Великую депрессию, показывает убыток. Годовая доходность в течение более длительных периодов менее изменчива, поскольку случайные движения рынка, а следовательно, и доходности, усредняются.

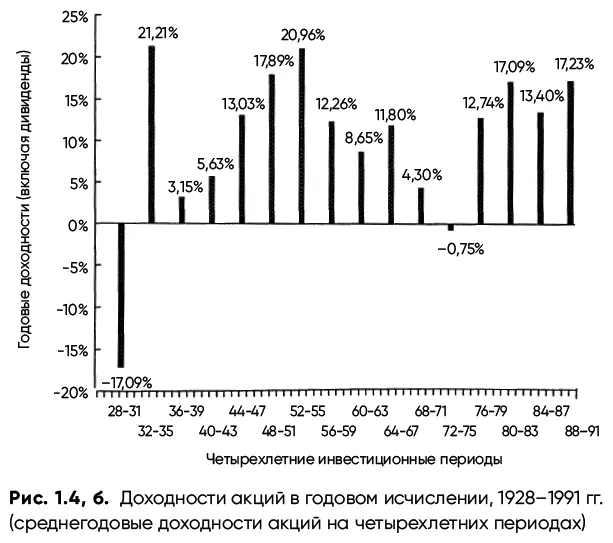
Мы можем также взглянуть на последние 64 года, начиная с 1928 г., поделенные на четырехлетние периоды. Результаты этого анализа приведены на рис. 1.4, б, и они немного отличаются. Хотя эти четырехлетние доходности все еще менее изменчивы, чем доходности за отдельные годы, но они показывают большее число убыточных периодов, чем предыдущий график.